2022-12-05

線形回帰（単回帰分析）を1から実装して理解を深めてみよう: つづき

この記事は、MATLAB アドベントカレンダー（その2）の5日目の記事として書かれています。

1 はじめに

前回の記事では、以下のように、線形回帰（単回帰分析）を行った時の、式の傾きや切片の求め方についてまとめました。

kentapt.hatenablog.com

例えば、以下の図では、y = 0.33x + 50.2 という式が得られています。この傾きや切片を、xとyのペアからどのように求めるか、ということでした。

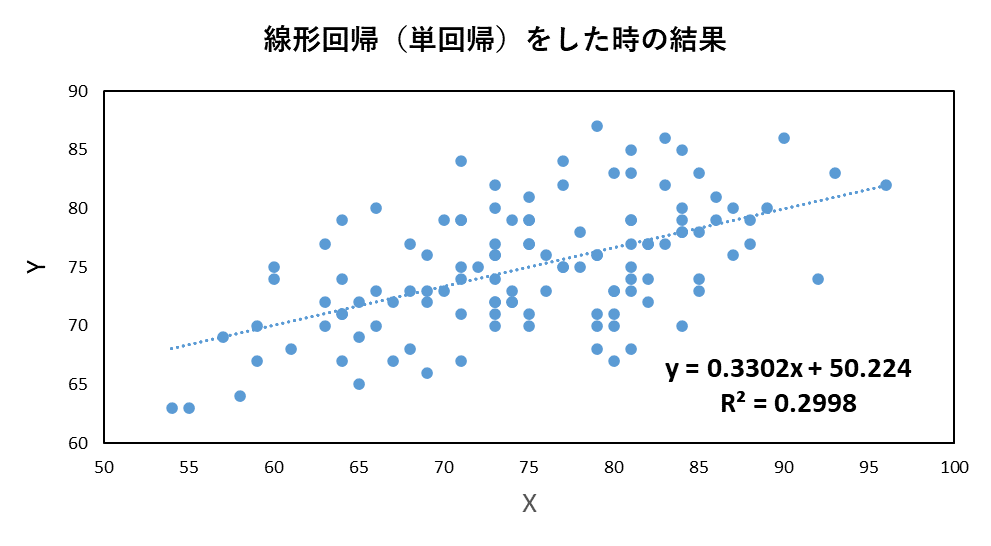
具体的には、傾きは、

$a\;=\;\frac{\sum_{i\;=\;1}^N x_i y_i \;-\frac{1}{N}\sum_{i\;=\;1}^N x_i \;\sum_{i\;=\;1}^N y_i }{\sum_{i\;=\;1}^N {x_i }^2 -\frac{1}{N}{\left(\sum_{i\;=\;1}^N x_i \;\right)}^2 }$

...(前回の記事の17)

であり、切片については以下の通りでした。

$b=-\frac{1}{N}\sum_{i\;=\;1}^N x_i \;\frac{\sum_{i\;=\;1}^N x_i y_i \;-\frac{1}{N}\sum_{i\;=\;1}^N x_i \;\sum_{i\;=\;1}^N y_i }{\sum_{i\;=\;1}^N {x_i }^2 -\frac{1}{N}{\left(\sum_{i\;=\;1}^N x_i \;\right)}^2 }+\frac{1}{N}\sum_{i\;=\;1}^N y_i \;$

...(前回の記事の18)

しかし、文量が多くなってしまい、上の図中にあるような、決定係数 $R^2$ の求めかたについては、触れられていませんでした。

そこで、本記事では、線形回帰（単回帰分析）をしたときの、決定係数の求め方について、簡単にまとめます。さらに、MATLABを用いてコーディングをし、ここでの理解による実装の結果と、MATLABのregress関数およびExcelの結果が一致することを確かめます。

本記事は、タイプミスや間違いなどがあるかもしれません。その場合教えていただけますと幸いです。

2 決定係数の求め方について

決定係数は、以下の図の、残差を利用して求めることができます。残差とは、予測値と実測値の差のことです。

この値が小さければ小さいほど、決定係数は高くなりそうです。では、具体的にどのような式で決定係数を求めるのか見ていきたいと思います。

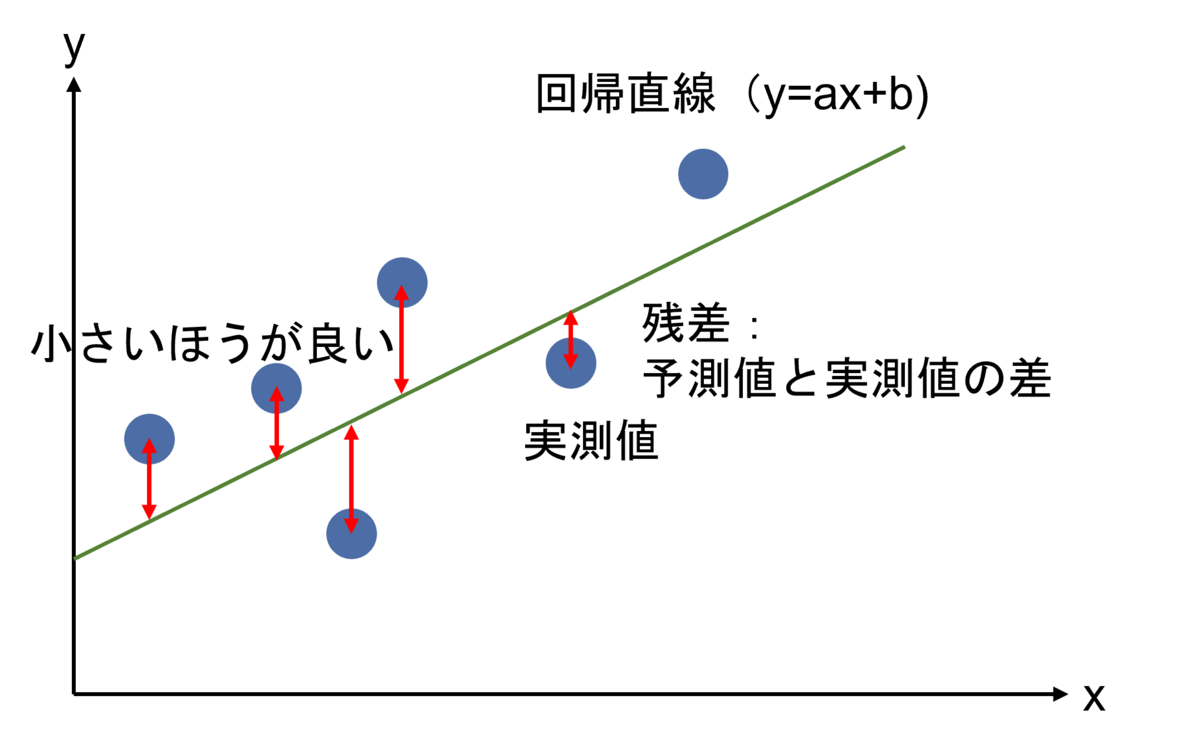
回帰分析における寄与率(=決定係数)と、残差や相関係数との関係を参考に作成

end0tknr.hateblo.jp

2.1. 偏差積和を用いた傾きと切片の式の展開

2.1.1. 傾きについて

以下のような、偏差積和を考えます。 $\bar{x}$ はxの平均です。yについても同様です。

各サンプルから、その $\bar{x}$ を引き算し、yについても同様の処理を行ったものとの積を求めます。それをサンプル全体に対して行い、和を取ります。

$T_{\textrm{xy}} =\sum_{i=1}^N \left(x_i -\bar{x} \right)\left(y_i -\bar{y} \right)$

...(1)

偏差積和についてはより詳しい内容を知りたい方は以下のページをご覧ください。

https://toukeigaku-jouhou.info/2017/06/24/variance-covariance/

(1)の中身を展開して、

$=\sum_{i=1}^N \left(x_i y_i -x_i \bar{\;y} -\bar{xy_i \;} +\bar{x\;} \bar{y} \right)$

...(2)

各項にばらして、

$=\sum_{i=1}^N x_i y_i \;-\sum_{i=1}^N x_i \bar{y} \;-\sum_{i=1}^N y_i \bar{x} \;+\sum_{i=1}^N \bar{x} \;\bar{y} \;$

...(3)

$=\sum_{i=1}^N x_i y_i \;-\bar{y} \sum_{i=1}^N x_i \;-\bar{x} \sum_{i=1}^N y_i \;+\sum_{i=1}^N \bar{x} \;\bar{y} \;$

xの和は、xの平均と個数を掛け合わせたものと等しいので、

$=\sum_{i=1}^N x_i y_i \;-\bar{y} N\bar{x} -\bar{x} N\bar{y} +N\bar{x} \;\bar{y}$

...(4)

$=\sum_{i=1}^N x_i y_i \;-N\bar{x} \;\bar{y}$

...(5)

となります。

Σの中に戻して、

$T_{\textrm{xy}} =\sum_{i=1}^N x_i y_i -\frac{1}{N}\;\sum_{i\;=\;1}^N x_i \;\sum_{i\;=\;1}^N y_i \;$

...(6)

を得ます。

傾きの式の分子に相当することがわかります。

$a\;=\;\frac{\sum_{i\;=\;1}^N x_i y_i \;-\frac{1}{N}\sum_{i\;=\;1}^N x_i \;\sum_{i\;=\;1}^N y_i }{\sum_{i\;=\;1}^N {x_i }^2 -\frac{1}{N}{\left(\sum_{i\;=\;1}^N x_i \;\right)}^2 }$

...(前回の記事の17)

次に、aの式の分母について考えます。

式(1)において、x = y であるとします。すると以下の等式が成り立ちます。

$\sum_{i=1}^N x_i x_i -\frac{1}{N}\;\sum_{i\;=\;1}^N x_i \;\sum_{i\;=\;1}^N x_i =\sum_{i=1}^N \left(x_i -\bar{x} \right)\left(x_i -\bar{x} \right)\;$

...(7)

式を整理すると、

$\sum_{i=1}^N {x_i }^2 -\frac{1}{N}\;{\left(\sum_{i\;=\;1}^N x_i \;\right)}^2 =\sum_{i=1}^N {\left(\left(x_i -\bar{x} \right)\right)}^2$

...(8)

となります。この左辺の式はaの分母と等しいことがわかります。

そのため、aは以下のように書き換えることができます。

$=\frac{\sum_{i=1}^N \left(x_i -\bar{x} \right)\left(y_i -\bar{y} \right)}{\sum_{i=1}^N {\left(x_i -\bar{x} \right)}^2 }$

...(9)

偏差積和を $T_{\textrm{xy}}$ のように表すとすると、

$=\frac{T_{\textrm{xy}} }{T_{\textrm{xx}} }$

...(10)

のように表せます。

さらに、偏差積和をサンプル数で割ると、共分散になるため、

$=\frac{T_{\textrm{xy}} \times \frac{1}{N}}{T_{\textrm{xx}} \times \frac{1}{N}}$

...(11)

$=\frac{S_{\textrm{xy}} }{S_{\textrm{xx}} }$

...(12)

とすることができます。ここでは、共分散を $S_{\textrm{xy}}$ のように表しています。

なお、式(10)から(12)にて扱ったような、共分散については以下のページがわかりやすかったです。

共分散の意味と簡単な求め方

manabitimes.jp

2.1.2. 切片について

切片は以下のようになるのでした。

$b=-\frac{1}{N}a\sum_{i\;=\;1}^N x_i \;+\frac{1}{N}\sum_{i\;=\;1}^N y_i \;$

...(前回の記事の14)

aにさきほどの式(12)の結果を代入します。

$b=-\frac{1}{N}\frac{S_{\textrm{xy}} }{S_{\textrm{xx}} }\sum_{i\;=\;1}^N x_i \;+\frac{1}{N}\sum_{i\;=\;1}^N y_i \;$

...(13)

一項目と二項目を入れ替えます。

$=\frac{1}{N}\sum_{i\;=\;1}^N y_i -\frac{1}{N}\sum_{i\;=\;1}^N x_i \;\times \;\frac{S_{\textrm{xy}} }{S_{\textrm{xx}} }$

...(14)

$\frac{1}{N}\sum_{i\;=\;1}^N x_i \;=\;\bar{x}$ という関係であるため、

$=\bar{y} -\frac{S_{\textrm{xy}} }{S_{\textrm{xx}} }\;\bar{x} \;\;$

...(15)

であることが言えます。

これにより、傾きと切片の式がかなり見やすくなりました。

決定係数を求めるために、最後の準備を行います。

2.2. 平方和の分解

y = ax+bの式では、xが大きくなるほど、yの値もaxだけ大きくなります。もし、この回帰式が完全である場合、yの変動は、xの変動によって

完全にカバーすることができます。しかし、実際は、ノイズなどの影響で、完全な式は得られることはなく、そのxの変動では説明できない部分が発生してしまいます。この説明できない部分が小さいほどうれしいです。では、このxの変動によって説明される部分と、説明されない部分をどのように切り分けるとよいでしょうか。

はじめに、

$y_i$ の平均回りの変動（平方和）は、説明変数 $y_i$ の変動によって説明される部分と、説明できない残差の平方和に分解することができます。

実際に計算していきます。 $y_i$ の平均回りの変動（平方和）は以下の通りです。

$S_{\textrm{yy}} =\;\sum_{i\;=\;1}^N {\left(y_i -\bar{y} \right)}^2$

...(16)

y = ax+bという式で回帰しているため以下のように記述できます。

$=\;\sum_{i\;=\;1}^N {\left\lbrace y_i -\left({\textrm{ax}}_i +b\right)+\left({\textrm{ax}}_i +b\right)-\bar{y} \right\rbrace }^2$

...(17)

展開して、

$=\;\sum_{i\;=\;1}^N {\left\lbrace y_i -\left({\textrm{ax}}_i +b\right)\right\rbrace }^2 +\;\sum_{i\;=\;1}^N {\left\lbrace \left({\textrm{ax}}_i +b\right)-\bar{y} \right\rbrace }^2 +2\sum_{i\;=\;1}^N \left\lbrace y_i -\left({\textrm{ax}}_i +b\right)\right\rbrace \left\lbrace \left({\textrm{ax}}_i +b\right)-\bar{\left.y\right\rbrace } \right.$

...(18-1)

ここで、式(18)の3つ目の項について考えます。

$\sum_{i\;=\;1}^N \left\lbrace y_i -\left({\textrm{ax}}_i +b\right)\right\rbrace \left\lbrace \left({\textrm{ax}}_i +b\right)-\bar{\left.y\right\rbrace } \right.$

...(18-2)

前回の記事で、回帰残差の和はゼロになることを確かめました。

kentapt.hatenablog.com

つまり、残差を以下のように定義したとします。

$e_i =y_i -\left({\textrm{ax}}_i +b\right)\;$

...(19-1)

すると、

$\sum_{i\;=\;1}^N e_i =0$

...(19-2)

が成り立ちます。

さらに、同様に前回の記事で、

回帰残差とxの値はベクトルとして直交していることも確かめました。

$\sum_{i\;=\;1}^N e_i x_i =0$

そのため、式(18)は、

$\sum_{i\;=\;1}^N e_i \left\lbrace \left({\textrm{ax}}_i +b\right)-\bar{\left.y\right\rbrace } \right.$

$=\left(b-\bar{y} \right)\sum_{i\;=\;1}^N e_i +a\;\sum_{i\;=\;1}^N e_i x_{i\;} =0$

...(19-3)

であることがわかります。そのため、この値は0になるため、式から除外します。

式(18-1)は以下のようになります。

$=\;\sum_{i\;=\;1}^N {\left\lbrace y_i -\left({\textrm{ax}}_i +b\right)\right\rbrace }^2 +\;\sum_{i\;=\;1}^N {\left\lbrace \left({\textrm{ax}}_i +b\right)-\bar{y} \right\rbrace }^2$

...(19-4)

さらに、式(19-4)の1項目について考えます。

$\sum_{i\;=\;1}^N {\left\lbrace y_i -\left({\textrm{ax}}_i +b\right)\right\rbrace }^2 \;$

...(20)

同様に、前回の記事で、推定された回帰直線は、サンプルのxとyの平均を通ることを確かめました。

そのため、式(20)は以下のように書き換えることができます。

$＝\;\sum_{i\;=\;1}^N {\left\lbrace y_i -\bar{y} -a\left(x-\bar{x} \right)\right\rbrace }^2 \;$

...(21)

この式を展開して、

$＝\;\sum_{i\;=\;1}^N {\left(y_i -\bar{y} \right)}^2 -2a\sum_{i\;=\;1}^N \left(x_i -\bar{x} \right)\left(y_i -\bar{y} \right)+a^2 \sum_{i\;=\;1}^N {\left(x_i -\bar{x} \right)}^2$

...(22)

第三項目の $a$ を１つだけ展開します。

$a\;=\frac{S_{\textrm{xy}} }{S_{\textrm{xx}} }$ であることを上で確かめました。そのため、

${=\;S}_{\textrm{yy}} -2aS_{\textrm{xy}} +a\frac{S_{\textrm{xy}} }{S_{\textrm{xx}} }S_{\textrm{xx}}$

...(23)

であり、二項目と三項目を計算できます。

${=\;S}_{\textrm{yy}} -aS_{\textrm{xy}}$

...(24)

この式の左辺の値（残差平方和）である、 $\sum_{i\;=\;1}^N {\left\lbrace y_i -\left({\textrm{ax}}_i +b\right)\right\rbrace }^2 \;$ を

${\;S}_e$ F

とします。

すると、　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

${\;S}_{\textrm{yy}} =aS_{\textrm{xy}} +{\;S}_e$

...(25)

とすることができます。 $S_R \;=aS_{\textrm{xy}}$ とすると、

${\;S}_{\textrm{yy}} ={\;S}_e +S_R$ 　　

...(26)

です。

ここで、以下の式がもとになっていました。

$S_{\textrm{yy}} \;=\;\sum_{i\;=\;1}^N {\left\lbrace y_i -\left({\textrm{ax}}_i +b\right)\right\rbrace }^2 +\;\sum_{i\;=\;1}^N {\left\lbrace \left({\textrm{ax}}_i +b\right)-\bar{y} \right\rbrace }^2$

...(19-4を再掲）

そして、

$\sum_{i\;=\;1}^N {\left\lbrace y_i -\left({\textrm{ax}}_i +b\right)\right\rbrace }^2 \;$

を ${\;S}_e$ とした場合、

${\;S}_{\textrm{yy}} ={\;S}_e +S_R$ 　

である関係式を得ました。

この関係式を19に代入すると、

$S_{\textrm{yy}} =\;{\;S}_{\textrm{yy}} -S_R +\sum_{i\;=\;1}^N {\left\lbrace \left({\textrm{ax}}_i +b\right)-\bar{y} \right\rbrace }^2 \;$

...(27)

であり、

$S_R =\sum_{i\;=\;1}^N {\left\lbrace \left({\textrm{ax}}_i +b\right)-\bar{y} \right\rbrace }^2$ 　　　　　　

...(28)

となります。

ここで、 $S_R \;=aS_{\textrm{xy}}$ と置いていました。

式(12)より、

$S_R =\frac{{S_{\textrm{xy}} }^2 }{S_{\textrm{xx}} }$

...(29)

です。

2.3. 決定係数の式の定義

式(26)を振り返ってみます。 ${\;S}_{\textrm{yy}} ={\;S}_e +S_R$ 　としたときの、 ${\;S}_{\textrm{yy}}$ は、目的変数yを二乗して足し合わせたもので、全変動を表しています。

また、 $S_e$ は残差平方和でした。つまり、（全変動）＝（残差平方和）＋　 $S_R$

となっており、 $S_R$ はデータの変動のうち、回帰直線によって表すことのできる量であると考えることができます。

そこで、決定係数 $R^2$ を、全変動のうち、回帰直線によって表すことのできる割合であるとし、大きい（最大1）ほどよいものになります。

式で表すと、

$R^2 =\frac{S_R }{{\;S}_{\textrm{yy}} }$

...(30)

となります。式(26)を利用して、

$=\frac{S_{\textrm{yy}} -S_e }{{\;S}_{\textrm{yy}} }=1-\frac{S_e }{{\;S}_{\textrm{yy}} }$

...(31)

となります。

これにより、決定係数を計算するための式を得ることができました。

2.4. 決定係数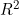 $R^2$ と相関係数rの関係

式(30)を以下のように変形します。

相関係数は、xとyの共分散である $S_{\textrm{xy}}$ をxとyの標準偏差で割ったものであるため、

$R^2 =\frac{S_R }{{\;S}_{\textrm{yy}} }=\frac{\frac{{S_{\textrm{xy}} }^2 }{S_{\textrm{xx}} }}{{\;S}_{\textrm{yy}} }={\left(\frac{S_{\textrm{xy}} }{\sqrt{S_{\textrm{xx}} S_{\textrm{yy}} }}\right)}^2 \;={r_{\textrm{xy}} }^2 \;$

...(32)

このような関係式を得ることができました。単回帰分析の場合は、相関係数を2乗とすると決定係数になることがわかりました。

相関係数については、以下のページがわかりやすかったです。

rikei-logistics.com

3. MATLABとExcelを用いて、2章の決定係数の式が正しいか確認してみよう

ここで、2章の結果が正しいかどうかを、実際にコーディングして確かめてみます。以下の3つの結果が同じになるかを検証します。

MATLABのregress関数にて、単回帰分析を行った場合の決定係数の値
Excelにて、単回帰分析を行った場合の決定係数の値
MATLABにて2章の結果を1から書いて計算させたときの決定係数の値

3.1. MATLABのregress関数にて、単回帰分析を行った場合の決定係数の値

load examgrades

yとXの値を設定します。

y = grades(:,5);
X = [ones(size(grades(:,1))) grades(:,1)];

regress関数で単回帰分析を行います。決定係数は0.2998でした。

[mdl,~,r,rint,stats] = regress(y,X);
disp(strcat('R2_MATLAB= ',string(stats(1))))

R^2=0.2998

3.2. Excelにて、単回帰分析を行った場合の決定係数の値

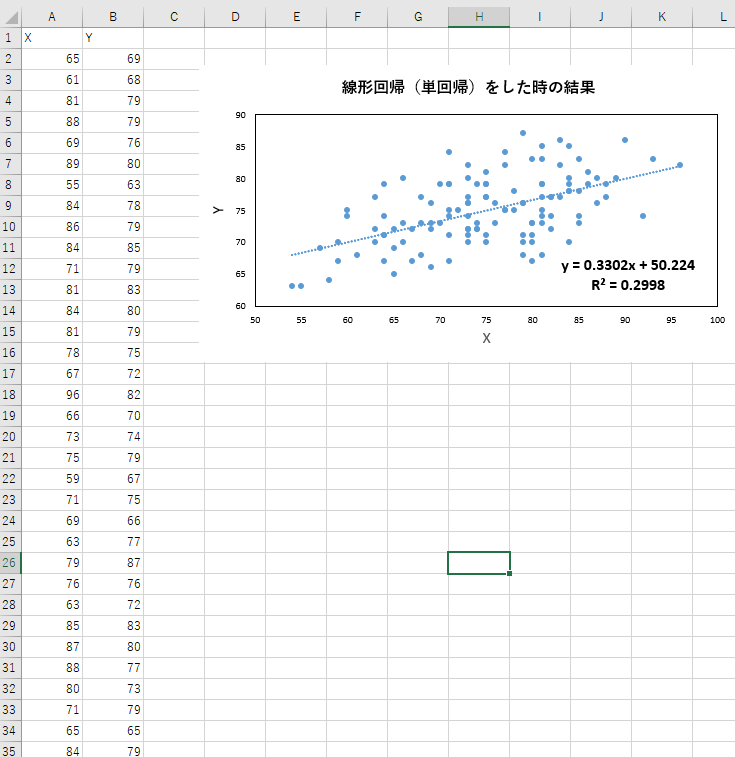
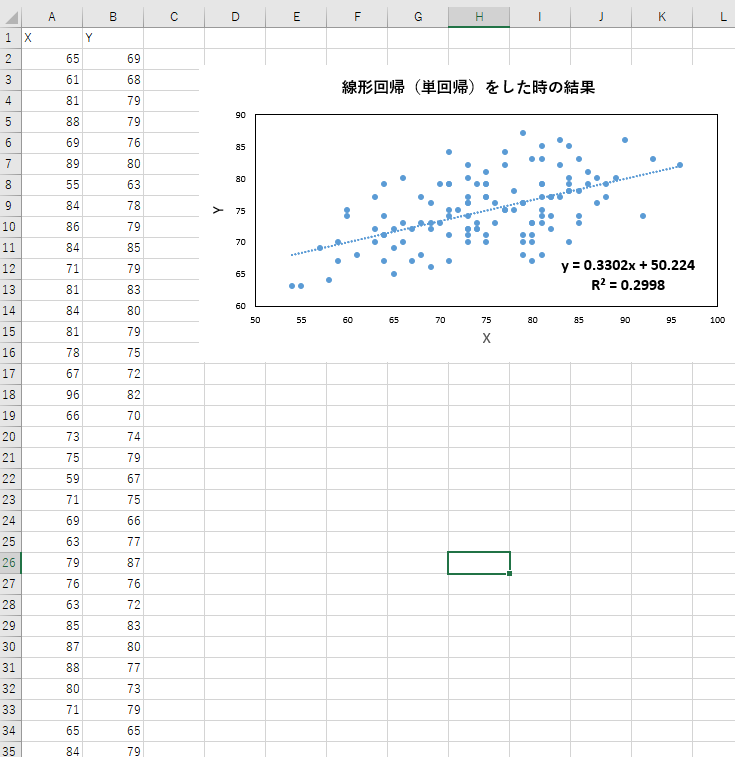
3.1にて用いたデータをコピーアンドペーストして、「近似曲線」の機能を用いて、

傾きと切片の値を計算しました。

3.1と同じ、決定係数の値が計算されており、まずは、3.1および3.2で、ソフトウェアの関数や機能にてうまく値が計算できたと思われます。

3.3. MATLABにて2章の結果を1から書いて計算させたときの決定係数の値

前回の記事で得た、

$a\;=\;\frac{\sum_{i\;=\;1}^N x_i y_i \;-\frac{1}{N}\sum_{i\;=\;1}^N x_i \;\sum_{i\;=\;1}^N y_i }{\sum_{i\;=\;1}^N {x_i }^2 -\frac{1}{N}{\left(\sum_{i\;=\;1}^N x_i \;\right)}^2 }$

...(前回の記事の17)

および

...(前回の記事の18)

を用いてまずは、傾きと切片の値を計算します。

さらに、(30)の $\frac{S_R }{{\;S}_{\textrm{yy}} }$ の値を計算します。

x = grades(:,1);
bunshi_a = sum(x.*y)-1/numel(x)*sum(x)*sum(y);
bumbo_a = sum(x.^2)-1/numel(x)*(sum(x)^2);
a = bunshi_a/bumbo_a;
b = -1/numel(x)*sum(x)*a+1/numel(x)*sum(y);
SR = sum((a*x+b-mean(y)).^2);
Syy = sum((y-mean(y)).^2);
R2 = SR/Syy

R2 = 0.2998

こちらも0.2988になり、正しいことがわかりました。

これらの結果から、2章の私の理解や、ここでのコーディングはおおよそ正しそうです。

4. 簡単なまとめ

この記事では、線形回帰（単回帰分析）における、決定係数の計算方法についてまとめました。
MATLABとExcelを用いて、ここでまとめた決定係数の式が正しいことを確認しました
普段から何気なく使っている決定係数ですが、丁寧に求めて記事にまとめるのが大変でした。しかし、これまでより広い視点で線形回帰を使えそうな気がしました。
（全変動）＝（残差平方和）＋（データの変動のうち、回帰直線によって表すことのできる量）という関係式を求め、決定係数の計算をしました。しかし、この式の導出は飛ばして、公式のような形で決定係数の定義を覚えて、決定係数の計算をしてしまってもいいかもしれません（？）

5. 参考文献（本文中に記載のないもの）

回帰直線の式を最小二乗法により計算する

ictsr4.com

永田靖、棟近雅彦共著：多変量解析入門

www.amazon.co.jp

2022-12-04

線形回帰（単回帰分析）を1から実装して理解を深めてみよう

統計機械学習 matlab

この記事は、MATLAB アドベントカレンダー（その2）の4日目の記事として書かれています。

qiita.com

1 はじめに

以下の図のように、エクセルなどで、直線で回帰（フィッティング）した経験がある方も多いかもしれません。

以下の図では、y = 0.33x + 50.2 という式が得られています。

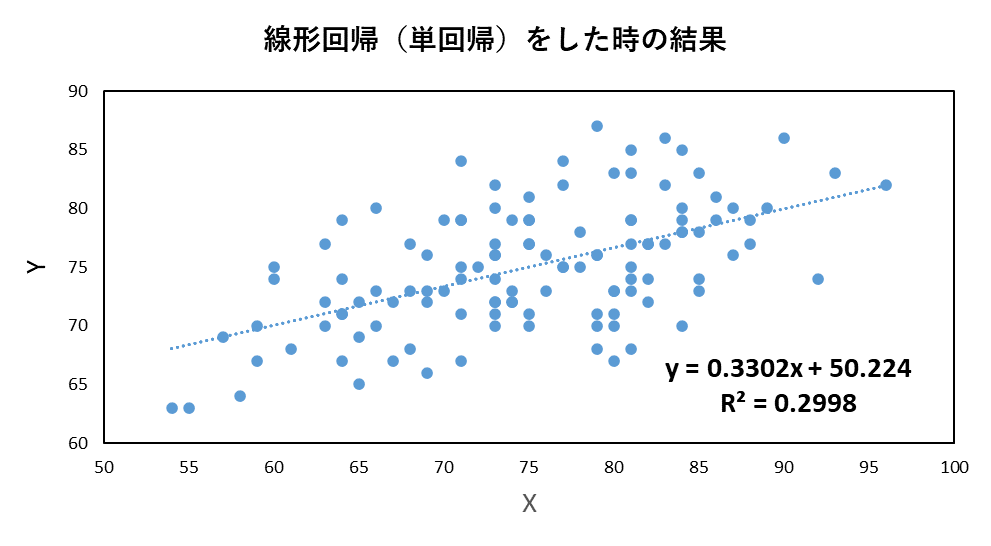
例えば、これにより、データ同士の相関関係を知ることができ、非常によく用いられる解析方法です。

このような線形回帰（単回帰）の説明としては、以下のページがわかりやすかったです。

回帰分析(単回帰分析)をわかりやすく徹底解説！

udemy.benesse.co.jp

実は簡単！　10分あれば回帰分析ができます

cacco.co.jp

よく用いられる手法ではありますが、それを実際に、導出し、自分の手で（プログラミングやExcelを使って）検算したことのある人は、

あまり多くないかもしれません。ここでは、自分の勉強のまとめとして、線形回帰の中でも、1つの変数を用いた、単回帰の導出を行い、さらに、複数の方法での実装（プログラミング）により自身の理解が正しいことを確認します。なお、実装による確認などを通して、検算はしていますが、間違いなどあるかもしれません。その場合は教えていただけますと幸いです。

この記事の原稿や、コード、検算用のExcelファイルは以下のページに格納されています。勉強の助けになれば幸いです。

github.com

また、線形回帰に関しては、本記事の内容は、最初の一歩のみを紹介しています。線形回帰を実際の研究や実務に利用したい方は、

以下の動画が大変参考になると思います。

www.youtube.com

2 解析方法

単回帰分析では、データによくあてはまる直線を考えます。以下に、そのイメージを示します。

直線は、数式で、y = ax+bという形で表すことができます。この直線を下の図では、緑で表しています。

単回帰分析では、この直線と、各サンプルとのちがい（残差）が最小になるような直線を求めます。

そのために、最小二乗法を用いていきます。

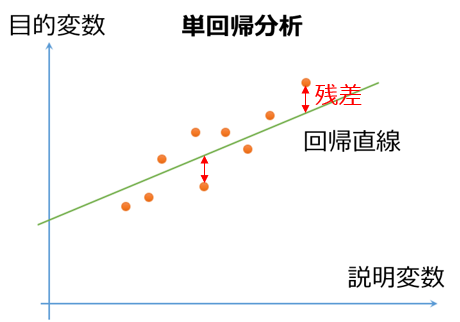
図出展：残差とは何か？正規分布していることの意味をわかりやすく解説！

best-biostatistics.com

最小二乗法については、以下の記事がわかりやすかったです。

最小二乗法（直線）の簡単な説明 | 高校数学の美しい物語

3 導出

3.1. aとbについて偏微分

サンプルのyの値と、回帰式によって求められた値（予測値）との差が小さくなることを目的とします。

差分については、単純に引き算をすると、マイナスになった場合とプラスになった場合で誤差が相殺されてしまうため、

それらの2乗の値を考えます。そして、この誤差の2乗の値の和（残差平方和）が最小となる、aとbを求めたいと思います。

aとbとは、さきほど示したような、y = ax+bの式の傾きと切片のことです。

この残差平方和をEとします。また、のちの計算結果をよりシンプルにするため、1/2を係数として付けておきます。

$E=\;\frac{1}{2}\sum_{i\;=\;1}^N {\left(y_i -\left({\textrm{ax}}_i +b\right)\right)}^2$

...(1)

このEを最小とするために、aとbの値について微分（偏微分）をして、そのときの値がゼロになるときのことを考えます。

ここで、(1)の中に含まれる以下の部分をXと置きます。

$X=\;{\textrm{ax}}_i +b$

...(2)

まずは、aについて偏微分することを考えます。

(2)のようにおいたため、(1)の式は、ある関数に別の関数が入っている関数になります。

そこで、以下のような、合成関数の微分を行います。

univ-juken.com

$\frac{\partial E}{\partial a}=\frac{\partial E}{\partial X}\frac{\partial X}{\partial a}\;$

... (3)

式(2)をaで微分すると、 $x_i$ であるため、(3)は以下のように展開できます。

$\frac{\partial E}{\partial a}\;=\frac{1}{2}\sum_{i\;=\;1}^N -2\left(y_i -X\right)x_i =\sum_{i\;=\;1}^N -\left(y_i -{\textrm{ax}}_i -b\right)x_i \;$

...(4)

各項を個別に分けて、

$=\sum_{i\;=\;1}^N {{\textrm{ax}}_i }^2 +\sum_{i\;=\;1}^N {\textrm{bx}}_i \;\;-\sum_{i\;=\;1}^N x_i y_i \;$

...(5)

(5)のようになりました。

同様に、以下の(1)式をbで偏微分します。

$E=\;\frac{1}{2}\sum_{i\;=\;1}^N {\left(y_i -\left({\textrm{ax}}_i +b\right)\right)}^2$

...(1を再掲）

という式において、ここでも以下のようにXを定める。

$X=\;{\textrm{ax}}_i +b$

...(2を再掲）

合成関数の微分の式は以下のようになる。

$\frac{\partial E}{\partial b}=\frac{\partial E}{\partial X}\frac{\partial X}{\partial b}\;$

...(6)

(2)式において、bにて微分を行うと、1になるため、

$\frac{\partial E}{\partial b}\;=\;\frac{1}{2}\sum_{i\;=\;1}^N -2\left(y_i -X\right)\left(1\right)=\sum_{i\;=\;1}^N -\left(y_i -{\textrm{ax}}_i -b\right)$

...(7)

となり、さらに式を整理すると、

$=\;\sum_{i\;=\;1}^N \left({\textrm{ax}}_i -y_i +b\right)$

...(8)

$=\;\sum_{i\;=\;1}^N {\textrm{ax}}_i -\sum_{i\;=\;1}^N y_i \;+\;\sum_{i\;=\;1}^N b$

...(9)

$=a\sum_{i\;=\;1}^N x_i -\sum_{i\;=\;1}^N y_i \;+b\sum_{i\;=\;1}^N 1$

...(10)

このようになります。

3.2. 正規方程式を解く

3.1での偏微分の結果を整理すると以下のような2つの式（正規方程式）を得ることができます。

$a\sum_{i\;=\;1}^N {x_i }^2 \;+b\sum_{i\;=\;1}^N x_i \;\;\;=\;\sum_{i\;=\;1}^N x_i y_i \;$

...(11)

$a\sum_{i\;=\;1}^N x_i \;+b\sum_{i\;=\;1}^N 1\;=\sum_{i\;=\;1}^N y_i$

...(12)

この(11)および(12)式を解くと、aとbの値、つまり、xとyの値が与えられたときの、

回帰式の傾きと切片を求めることができます。

(12)式の2項目はbNであるため、

$a\sum_{i\;=\;1}^N x_i \;+bN=\sum_{i\;=\;1}^N y_i$

...(13)

となります。この式をbについて解いて、

$b=-\frac{1}{N}a\sum_{i\;=\;1}^N x_i \;+\frac{1}{N}\sum_{i\;=\;1}^N y_i \;$

...(14)

を得ることができます。

この(14)を(11)に代入します。

$a\sum_{i\;=\;1}^N {x_i }^2 \;+\left(-\frac{1}{N}a\sum_{i\;=\;1}^N x_i \;+\frac{1}{N}\sum_{i\;=\;1}^N y_i \right)\sum_{i\;=\;1}^N x_i \;\;\;=\;\sum_{i\;=\;1}^N x_i y_i \;$

...(15)

さらに、aについてまとめて、

$a\left(\sum_{i\;=\;1}^N {x_i }^2 -\frac{1}{N}{\left(\sum_{i\;=\;1}^N x_i \;\right)}^2 \right)\;=\sum_{i\;=\;1}^N x_i y_i \;-\frac{1}{N}\sum_{i\;=\;1}^N x_i \;\sum_{i\;=\;1}^N y_i$

...(16)

となります。

さらにaについて解くことで、

$a\;=\;\frac{\sum_{i\;=\;1}^N x_i y_i \;-\frac{1}{N}\sum_{i\;=\;1}^N x_i \;\sum_{i\;=\;1}^N y_i }{\sum_{i\;=\;1}^N {x_i }^2 -\frac{1}{N}{\left(\sum_{i\;=\;1}^N x_i \;\right)}^2 }$

...(17)

となりました。この結果を(14)に代入して、

...(18)

となりました。これにより、傾きと切片の値を求めることができました。

4. コーディングをもとに検算

ここで、3章の結果が正しいかどうかを、実際にコーディングして確かめてみます。以下の3つの結果が同じになるかを検証します。

1 MATLABのregress関数にて、単回帰分析を行った場合の傾きと切片の値

2 Excelにて、単回帰分析を行った場合の傾きと切片の値

3 MATLABにて3章の結果を1から書いて計算させたときの、傾きと切片の値

4.1. MATLABのregress関数にて、単回帰分析を行った場合の傾きと切片の値

MATLABにて、デフォルトで読み込み可能な、examgradsデータを利用します。ここでは、データの内容については飛ばし、

傾きと切片の値が一致するかを検証します。

データをロードします。

load examgrades

yとXの値を設定します。

y = grades(:,5);
X = [ones(size(grades(:,1))) grades(:,1)];

regress関数で単回帰分析を行います。

[mdl,~,r,rint] = regress(y,X);

傾きの値 0.3302

    切片の値 50.2237

このように、傾きと切片の値をMATLABの関数で計算できました。次はExcelにて同様の計算を行います。

4.2 Excelにて、単回帰分析を行った場合の傾きと切片の値

4.1にて用いたデータをコピーアンドペーストして、「近似曲線」の機能を用いて、

傾きと切片の値を計算しました。

4.1と同じ、傾きと切片の値が計算されており、まずは、4.1および4.2で、ソフトウェアの関数や機能にてうまく値が計算できたと思われます。

4.3 MATLABにて3章の結果を1から書いて計算させたときの、傾きと切片の値

ここが本番の計算です。さきほど導出した、(17) (18)式を用いて、傾きと切片の値を計算します。

$a\;=\;\frac{\sum_{i\;=\;1}^N x_i y_i \;-\frac{1}{N}\sum_{i\;=\;1}^N x_i \;\sum_{i\;=\;1}^N y_i }{\sum_{i\;=\;1}^N {x_i }^2 -\frac{1}{N}{\left(\sum_{i\;=\;1}^N x_i \;\right)}^2 }$

...(17を再掲)

...(18を再掲)

以下のように短い行数で書いてみます。

x = grades(:,1);
bunshi_a = sum(x.*y)-1/numel(x)*sum(x)*sum(y);
bumbo_a = sum(x.^2)-1/numel(x)*(sum(x)^2);
a = bunshi_a/bumbo_a

a = 0.3302

b = -1/numel(x)*sum(x)*a+1/numel(x)*sum(y)

b = 50.2237

さきほどの、4.1および4.2での結果と一致しました。3章での計算が正しかったと考えられます。

ひとまず、ここまでで、簡単にですが、単回帰分析について、第一段階の理解ができたことにします。

5. 行列を用いて解いた場合

4章では、3章の理解が正しいことを確かめることができました。

今回用いているMATLABでは、行列計算がやりやすいです。

そこで、3章で出てきた正規方程式を振り返ります。

$a\sum_{i\;=\;1}^N {x_i }^2 \;+b\sum_{i\;=\;1}^N x_i \;\;\;=\;\sum_{i\;=\;1}^N x_i y_i \;$

...(11の再掲)

$a\sum_{i\;=\;1}^N x_i \;+b\sum_{i\;=\;1}^N 1\;=\sum_{i\;=\;1}^N y_i$

...(12の再掲)

上の連立方程式は、以下のように行列をもって表すことができます。

$\left\lbrack \begin{array}{cc} \sum_{i\;=\;1}^N {x_i }^2 & \sum_{i\;=\;1}^N x_i \;\;\\ \sum_{i\;=\;1}^N x_i & \sum_{i\;=\;1}^N 1\; \end{array}\right\rbrack \left\lbrack \begin{array}{c} a\\ b \end{array}\right\rbrack =\left\lbrack \begin{array}{c} \sum_{i\;=\;1}^N x_i y_i \;\\ \sum_{i\;=\;1}^N y_i \end{array}\right\rbrack$

...(19)

逆行列を用いて、aとbは以下のように求めることができます。

$\left\lbrack \begin{array}{c} a\\ b \end{array}\right\rbrack ={\left\lbrack \begin{array}{cc} \sum_{i\;=\;1}^N {x_i }^2 & \sum_{i\;=\;1}^N x_i \;\;\\ \sum_{i\;=\;1}^N x_i & \sum_{i\;=\;1}^N 1\; \end{array}\right\rbrack }^{-1} \left\lbrack \begin{array}{c} \sum_{i\;=\;1}^N x_i y_i \;\\ \sum_{i\;=\;1}^N y_i \end{array}\right\rbrack \;$

...(20)

この計算は、以下のように簡単に実行可能です。

ab = inv([sum(x.^2) sum(x); sum(x) numel(x)])*[sum(x.*y);sum(y)]

ab = 2x1    
    0.3302
   50.2237

このように、行列を用いた計算でも、正しく傾きと切片の値を計算できています。

今回は、単回帰分析で、変数が2つしかなかったため、3章のように解くことができましたが、

より多くの変数になると大変です。行列式を用いた導出や計算は非常に有効です。

6. 単回帰分析の性質の例

6.1 推定された回帰直線は、サンプルのxとyの平均を通る

切片の値は(14)で以下のように示されることがわかりました。

$b=-\frac{1}{N}a\sum_{i\;=\;1}^N x_i \;+\frac{1}{N}\sum_{i\;=\;1}^N y_i \;$

すると、回帰式は、

$y=\textrm{ax}+b=\textrm{ax}-\frac{1}{N}a\sum_{i\;=\;1}^N x_i \;+\frac{1}{N}\sum_{i\;=\;1}^N y_i$

...(21)

となり、さらにaについて整理すると、

$y=a\;\left(x-\frac{1}{N}\sum_{i\;=\;1}^N x_i \;\right)+\frac{1}{N}\sum_{i\;=\;1}^N y_i$

...(21)

となる。

$\frac{1}{N}\sum_{i\;=\;1}^N x_i \;$ 　および　 $\frac{1}{N}\sum_{i\;=\;1}^N y_i$ は、xやyを全て足して、サンプル数で割った値、つまり平均です。

そのため、

y = a(x-xの平均)+(yの平均)　となり、つまり、

推定された回帰直線は、サンプルのxとyの平均を通るということがわかります。

6.2 回帰残差の和はゼロとなる

単回帰分析にて、回帰を行っても、完全には説明できず、実際の値と、回帰した時の値の差（回帰残差 residual）が生まれます。

導出においては、この残差の二乗の和が最小になるようにしていました。

ここでは、この残差（2乗をしない）の和について考えます。

図出展：残差プロット

https://corvus-window.com/all_residual-plot/

以下のように、導出の段階で得た正規方程式を変形させてみます。

$a\sum_{i\;=\;1}^N x_i \;+b\sum_{i\;=\;1}^N 1\;=\sum_{i\;=\;1}^N y_i$

...(12の再掲)

$\sum_{i\;=\;1}^N \left.{\left(y\right.}_i -ax_i -b\right)=0$

...(22)

という式を得ることができました。

つまり、観測値yと回帰式によって得た値の差分をとり、それをサンプル数だけ足していくと0になります。つまり、

回帰残差の和はゼロとなることがわかりました。

6.3 回帰残差とxの値はベクトルとして直交している

6.2と同様に、以下の正規方程式を変形します。

$a\sum_{i\;=\;1}^N {x_i }^2 \;+b\sum_{i\;=\;1}^N x_i \;\;\;=\;\sum_{i\;=\;1}^N x_i y_i \;$

...(11の再掲)

$\sum_{i\;=\;1}^N \left.{\left(y\right.}_i -ax_i -b\right)x_i =0$

...(23)

つまり、回帰残差とxの値の内積がゼロであり、直交しているということを示しています。

7. 疑問点：線形回帰と主成分分析では何が異なるのか

主成分分析では、以下のように、その軸の分散が最大になるように、新たな軸を作っていました。

以下の図の、十字の軸は、線形回帰のときの回帰直線に似ています。

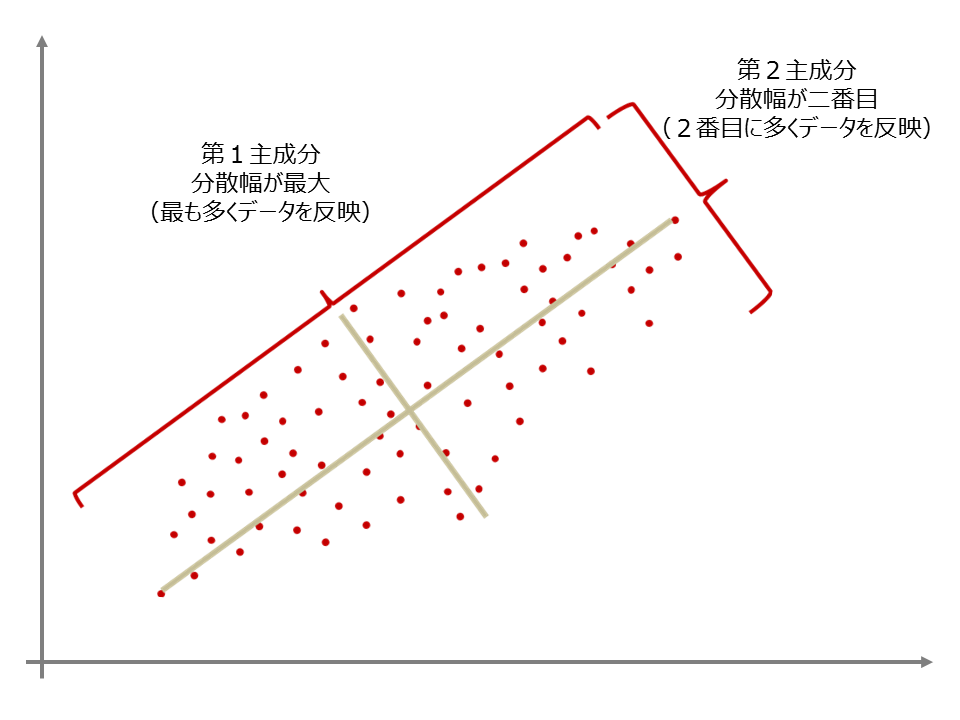
画像出典：株式会社インテージさま：主成分分析とは

https://www.intage.co.jp/glossary/401/

主成分分析については、私の過去の記事も見ていただけますと幸いです。

https://kentapt.hatenablog.com/entry/2022/02/16/182532

調べてみると、以下のようなわかりやすい資料がありました。

以下の文章および図は、浅野晃先生、応用統計学（2008 年度前期）　第６回(08. 5. 15)からの引用です。

=====引用開始=====

「分散が最大の軸」という表現で第１主成分を表現しましたが，もっと明確にいえば「多次元データを，それらがもつ価値をなるべく損なわないように，１次元の値（主成分得点）に縮約したもの」ということができます．また，図3 から明らかなように，第１主成分に投影することによって生じた価値の損失は，第２主成分によって表現されていることがわかります．ところで，この「各データと，その軸上への投影とのへだたりの２乗の合計が最小」という考え方は，回帰直線による直線のあてはめとよく似ています．回帰分析では，被説明変数の分散を，回帰直線からみた分散で何パーセント表現できるかを，回帰直線の当てはまり具合と考え，決定係数で表しました．しかし，両者の間には大きく違うところがあります（図5）．図3 からわかるように，主成分分析では，各データから第１主成分軸に垂線を下ろしたときの，各垂線の長さの２乗を最小にしています．これに対して，回帰分析では，各データから回帰直線に対してx1 軸に垂直に線分をひき，その長さの２乗を最小にしています．回帰分析では「x1 でx2 を説明する」あるいは「x1 からx2 を予想する」という考えにもとづいており，説明変数と被説明変数の区別があるので，x2 軸に沿ったへだたりを計算しています．主成分分析ではこのような区別はなく，どちらでどちらを説明しているわけでもないので，軸と各データとの「距離」を最小化の対象としています．

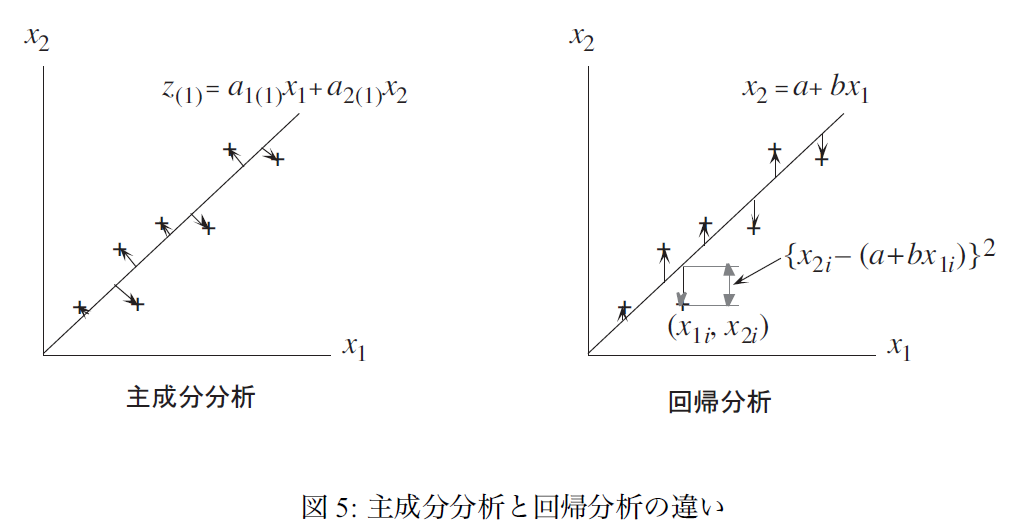
=====引用終了=====

「回帰分析では「x1 でx2 を説明する」あるいは「x1 からx2 を予想する」という考えにもとづいており」という点と、主成分分析ではそのような関係は想定しておらず、新たな主成分軸と各データとの距離そのものに主眼がおかれている、という点が納得がいき、非常に勉強になりました。

以下の、記事でも、回帰直線への垂線の長さを最小化する問題を解くと、ラグランジュの未定乗数法に

https://takmin.hatenablog.com/entry/2020/09/17/135353

8. その他：ガウスとルジャンドルとの論争

最小二乗法の発見に関しては以下のようなストーリーがあるそうです。以下の文章は入門統計学から引用しています。

=====引用開始=====

最小二乗法は、ドイツの天才学者であるガウスが小惑星セレスの軌道の計算に使ったことが始まりであると現在では知られています(1801年)。しかしガウスは自分の業績を公表することに無頓着でした。そのため、ルジャンドルというフランスの数学者がガウスよりも先（1805年）に論文として同様の理論を発表してしまい、他の数学者も巻き込んでの大論争になってしまいました。

=====引用終了=====

https://www.amazon.co.jp/%E5%85%A5%E9%96%80-%E7%B5%B1%E8%A8%88%E5%AD%A6-%E2%88%92%E6%A4%9C%E5%AE%9A%E3%81%8B%E3%82%89%E5%A4%9A%E5%A4%89%E9%87%8F%E8%A7%A3%E6%9E%90%E3%83%BB%E5%AE%9F%E9%A8%93%E8%A8%88%E7%94%BB%E6%B3%95%E3%81%BE%E3%81%A7%E2%88%92-%E6%A0%97%E5%8E%9F-%E4%BC%B8%E4%B8%80/dp/4274068552

9. 簡単なまとめ

この記事では、1変数のみの回帰直線の係数の計算方法（単回帰による回帰直線の傾きと切片の計算方法）についてまとめました。

私の理解による結果と、MATLABやExcelによる計算結果が一致しており、よかったです。

決定係数といった他の重要な事項に触れることができませんでしたが、今回は記事が長くなってしまったため、ひとまずここで一区切りとしたいと思います。今回の勉強にあたり、本文にて紹介した皆様の情報が非常に頼りになりました。ありがとうございました。

10. 参考文献（本文中に記載のないもの）

最小二乗法の基礎を丁寧に

qiita.com

回帰直線の式を最小二乗法により計算する

ictsr4.com

ガウスとルジャンドルとの論争について

ill-identified.hatenablog.com

永田靖、棟近雅彦共著：多変量解析入門

多変量解析法入門 (ライブラリ新数学大系) | 靖, 永田, 雅彦, 棟近 |本 | 通販 | Amazon

東京大学教養学部統計学教室 (編集)　統計学入門 (基礎統計学Ⅰ)

統計学入門 (基礎統計学Ⅰ) | 東京大学教養学部統計学教室 |本 | 通販 | Amazon

最小二乗法① 数学的性質　経済統計分析 (2013年度秋学期)

http://www2.toyo.ac.jp/\textasciitilde{}mihira/keizaitoukei2014/ols1.pdf

MATLAB ドキュメンテーション：regress

jp.mathworks.com

2022-12-03

iPhone LiDARで取得した3次元点群を地図上にプロットしてみよう

3次元点群 GIS matlab

この記事は、MATLAB アドベントカレンダー3日目の記事として書かれています。

qiita.com

この記事では、iPhone LiDARで取得した3次元点群をMATLABにて読み込み、さらに、地図（地球）上で可視化する方法について紹介します。言語はMATLABを使用します。

3次元点群を取得するためのアプリはScaniverseを用いました。

scaniverse.com

詳しい使い方は、以下の記事がわかりやすかったです。ここでは、すでにiPad LiDARにて計測し、PCに転送した状態から始めます。

note.com

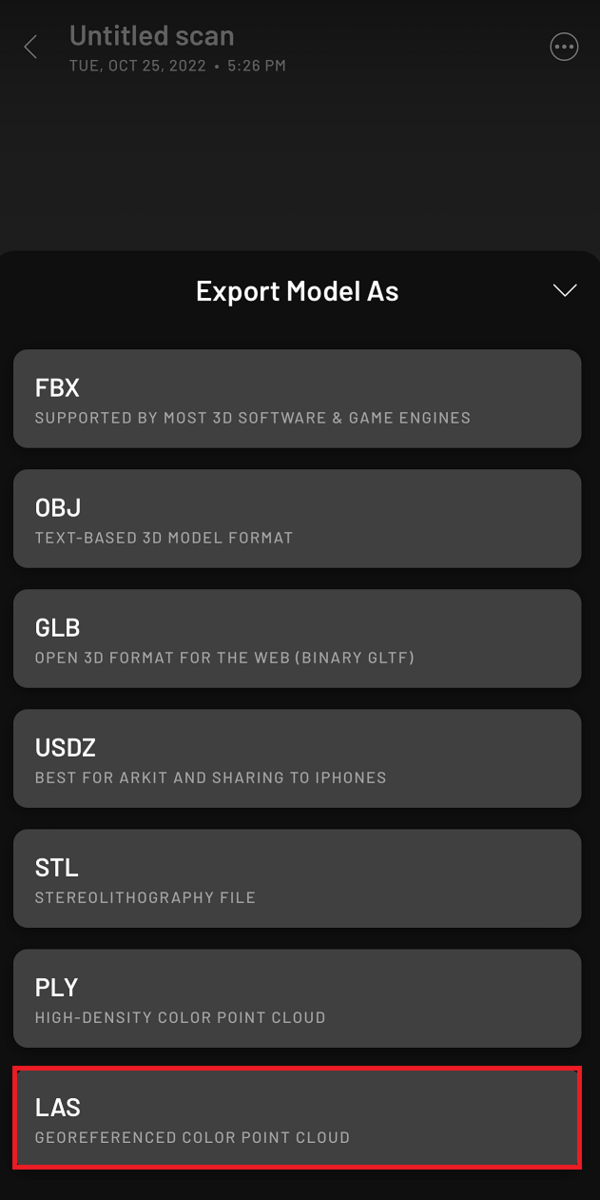
PCに転送（エキスポート）する方法は以下の図の通りです。右下のShareボタンから行うことができます。

なお、3次元モデルをエキスポートする際は、一番下のLAS形式を選択してください。

なお、ここで用いたコードや、点群ファイルは以下のページにアップロードされています。ぜひ、ダウンロードしてお使いください。

github.com

点群ファイルの読み込み

LiDAR toolboxの機能を用いて、点群データの読み込みを行います。以下のように、lasFileReaderやreadPointCloud関数を用いて、簡単に点群ファイルを読み込むことができます。

clear;clc;close all
% las/lazファイルを読み込むためのlasFileReader objectを作成する
lasReader = lasFileReader('treeTrunk.laz');
% las/lazファイルの、xyzおよび色情報を読み込み
ptCloud = readPointCloud(lasReader);
% 可視化
figure('Visible','on');pcshow(ptCloud)

以下のように、複雑な3次元形状を有する、樹木の幹部分をきれいに点群化できていることがわかります。iPhone LiDARとアプリ（Scaniverse）を用いることで、お手軽にこのようにきれいな点群を取得できるのは素晴らしいです。

座標系の変換

projcrsオブジェクトの作成

2022年12月においては、Scaniverseで、点群を取得し、エキスポートする場合（LAS形式）、経度・緯度ではなく、2次元平面に投影した方式でxy座標が保存されます。

具体的には、点群の座標は、東京で取得された場合、UTM N54（EPSGコード：32654）でエキスポートされます。後で用いる、geoplot関数との兼ね合いのため、これを経度・緯度に変換します。

projcrs関数に、EPSGコードを入力します。その結果、projcrsオブジェクトを作成することができます。

% projcrsオブジェクトを作成する
utm54N = projcrs(32654);
% 確認のため、CRSを表示
utm54N.GeographicCRS.Name

ans = "WGS 84"

UTMは、ユニバーサル横メルカトル（Universal Transverse Mercator）の略です。地球はおおよそ球形で、地球上の対象の座標は、3次元的に表すことができますが、それを2次元平面の投影しています。UTMはその投影方法の1つです。詳しい内容については、以下のページをご参照ください。

www.gsi.go.jp

projcrsオブジェクトの中身は以下のようになっています。Nameには、投影方法が書いています。lengthUnitでは、単位（メートル）が、ProjectionMethodには、投影方法が書いています。

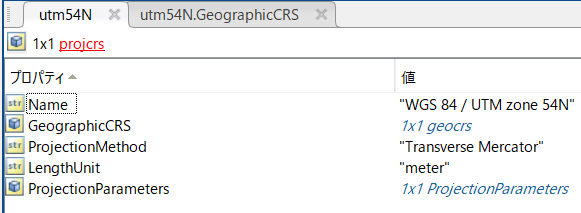
さらに、ここの、GeographicCRSは、geocrsオブジェクトが格納されており、その中身は以下のようになっています。

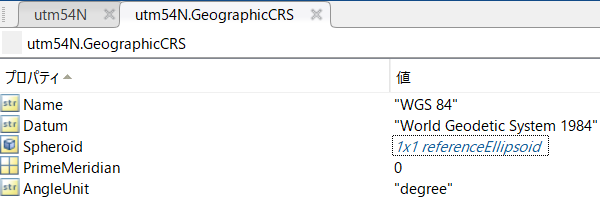
WGS 84についてですが、地球はおおよそ球体をしており、それを数式などを使ってモデル化することで、測量を行うことができます。そのモデル化の方式には、日本測地系や世界測地系といった様々なものがあります。WGS 84は世界測地系の中の1つの方式です。

この説明については、以下のページがわかりやすかったです。

club.informatix.co.jp

経度・緯度への変換

ここまで、iPhone LiDARの結果の表現に用いられた投影方法を表すオブジェクトを作成していました。次は、projinv関数を用いて、utm54Nのxy座標を経度・緯度に変換します。経度・緯度に変換することで、簡単に地図上にiPhone LiDARの点群の情報をプロットすることができます。

そして、この結果の可視化は、geoplot関数で行うことができます。

[lat,lon] = projinv(utm54N,ptCloud.Location(:,1),ptCloud.Location(:,2));
figure; geoplot(lat,lon)
% hold on;geobasemap('streets')
hold on;geobasemap('topographic')

上のようなプロットができましたが、これではどういう情報がプロットされているのかよくわかりません。もう少しズームアウトしてみます。

地図の上に、さきほどの樹木の幹の点群がプロットされていることがわかります。位置に関しても、この点群が取得された、東京都の代々木公園に正しくプロットされています。

ベースマップ（地図の種類）を変更するために、以下のように、geobasemapの中身を他のベースマップの種類を指定することもできます。

geobasemap('topographic')

さきほどの初めの図は少しわかりにくかったですが、このプロットの結果は樹木の点群を上から見た時の様子を示しているものだとわかります。

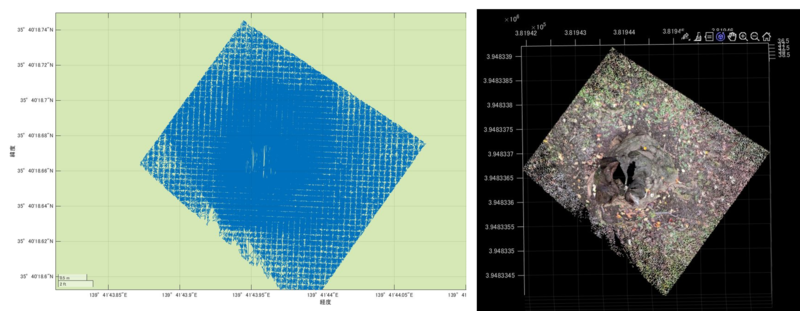
3次元マップでの点群の可視化

さきほどは、地図上にて、点群を可視化しましたが、2次元のマップであったため、各点の位置やその上からの様子を知るということに限定されていました。これでは、iPhone LiDARで取得した3次元情報をうまく可視化できているとは言えません。このセクションでは、iPhone LiDARで取得した点群を、3次元のマップ上で可視化してみます。

% 25点のうち1点のみを表示する。重くなってしまうため。
mskip = 1:25:length(lat);
% 3Dで可視化するための図を用意する
uif = uifigure;
g = geoglobe(uif);
% プロット
geoplot3(g,lat,lon,ptCloud.Location(:,3)-mean(ptCloud.Location(:,3)),'r','MarkerSize',2,'Marker','o','HeightReference','terrain','LineStyle','none','MarkerIndices',mskip)

可視化している様子は以下の動画をご覧ください。

www.youtube.com

このように、3Dの地図（ベースマップ）上で、iPhone LiDARの点群を可視化することができました。

色はうまく表示できていませんが、ベースマップ上でどのような点群が取得されたかを確認することができます。

いくつか注意点があるので記述します。

r: プロットの色。各点を実際の3Dの色付けを行うことができない。指定した1つの色のみの可視化になる
'LineStyle','none': これにより、独立した点（線でない）をプロットできる
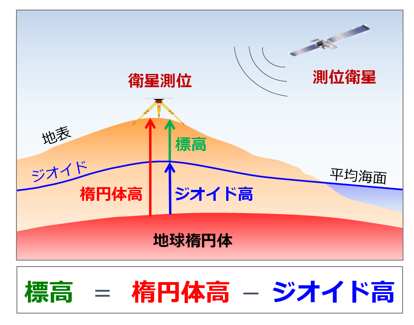
'HeightReference','terrain': 高さの基準を設定する。このほかに、'geoid' や'ellipsoid'が選択可能である。それぞれの違いについては、以下の図を参照して下さい。
'MarkerIndices'にて間引きを行わないと、表示が非常の重くなるため注意する必要がある。

図表出展: 国土地理院ジオイドとは

www.gsi.go.jp

まとめ

この記事では、iPhone LiDARで取得した点群をMATLABを用いて、地図上で可視化しました
投影座標系から経度・緯度への変換も簡単に行うことができました
3Dのベースマップ上で、点群を可視化することができました
表示する点数が多くなると、非常にビューワーが重くなるため、間引くことが必要です
容量の大きな点群や色付きの点群を閲覧することが難しいという課題はありますが、3次元データをスマホで取得し、お手軽にMATLABで遊べるという点が非常によかったです

参考にしたページ（本文中に記載がないもの）

jp.mathworks.com

2022-10-16

FLIRカメラで取得した熱画像をRGB画像に変換してみよう

1. はじめに

この記事では、FLIR社の赤外線カメラを用いて、取得した画像をRGB画像に変換する方法について述べます。ここでは、Pythonを用います。

赤外線カメラの詳細や、そのカメラの応用事例については以下のページが参考になりました。

atcl-dsj.com

本記事では、FLIR社製の赤外線カメラを用います。以下に、そのカメラの例を掲載します。

画像出展

www.flir.jp

FLIR社の赤外線カメラで取得した画像の例を以下に示します。温度によって、色分けされて示されています。この画像では、約22度から27度の範囲の温度が観測されています。

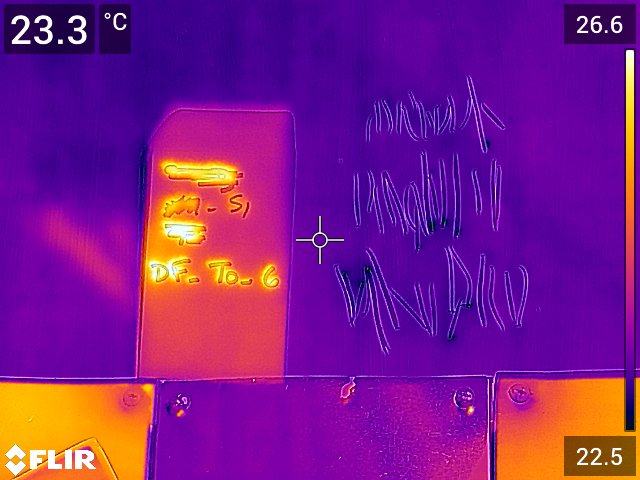
また、このカメラは、同時にRGB画像（色画像）を取得している場合が多く、この温度情報を持った画像をRGB画像に変換することができます。

その変換は、以下のFLIR Toolsと呼ばれるソフトウェアを用いて行うことができます。FLIR Toolsのインストール方法は以下のページをご覧ください。

flir-jp.custhelp.com

また以下の動画もわかりやすかったです。

www.youtube.com

このソフトウェアを用いて、以下のように、赤外線カメラの画像をRGB画像に変換することができます（以下の図はイメージです）。

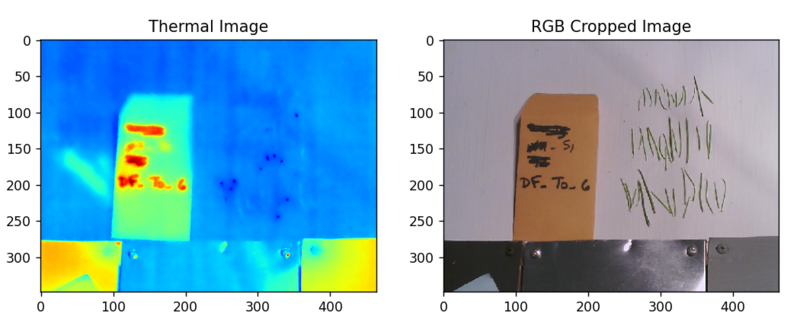
また、各ピクセルの持つ温度の値もCSVファイルとして取り出すことができます。

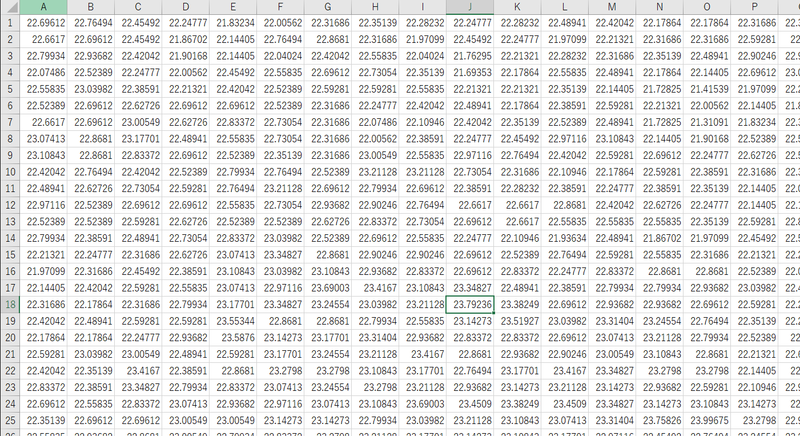
しかし、FLIR Toolsでは、1枚ずつ、読み込み、作業をすることが必要で、大量の画像をまとめて、同じ処理を繰り返すことは難しいです。

そこで、本記事では、以下のレポジトリを用いて、赤外線カメラの画像を、RGB画像に変換し、さらに、温度情報のCSVファイルを自動保存する方法について述べます。

なお、本記事で用いている画像やコードも以下のレポジトリのサンプルを用いています。

github.com

また、上のレポジトリをフォークし、少しアレンジを加えたものが以下のページで、本記事で用いるコードや原稿はここにアップロードされています。

github.com

2. 環境構築について

2.1. Exif toolのダウンロード

exiftoolの概要やそのダウンロードの方法や使い方は以下のページに記載しています。

kentapt.hatenablog.com

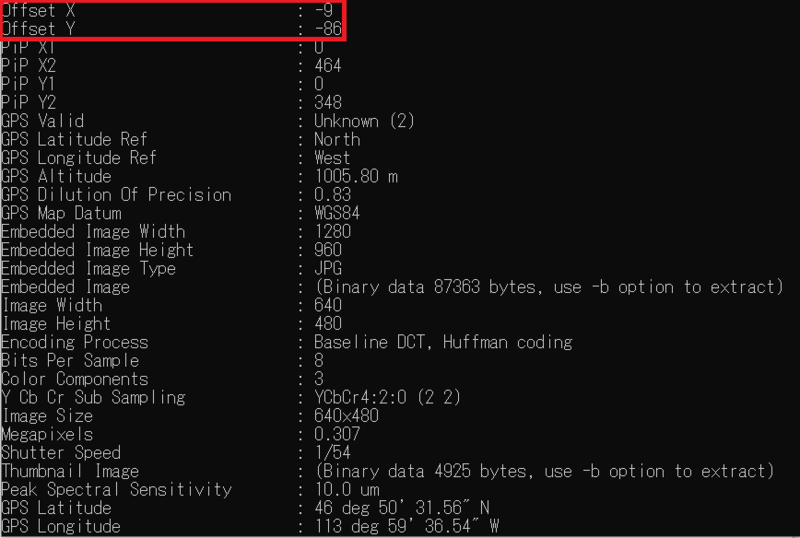
exiftoolを用いて、赤外線カメラの画像のメタ情報を取得した時の結果の例です。取得したカメラのモデル情報なども記載されていることがわかります。

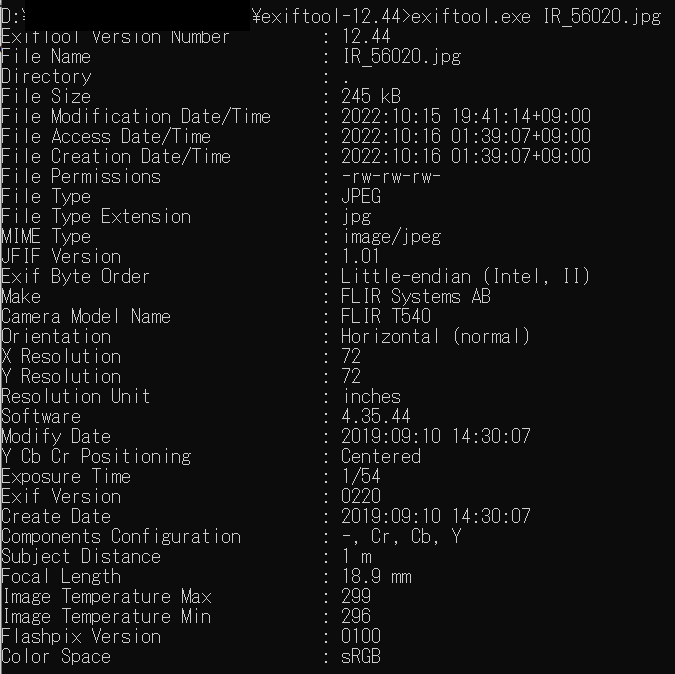
2.2. Pythonの実行環境について

まずは、このレポジトリのファイルをダウンロードします。

github.com

環境構築については、以下の2つの方法を紹介します。

必要なパッケージをインストールする
私の作ったanaconda環境をそのまま自分のPCに複製する

2の方法が簡単ですが、OSの違いなどで複製できない場合もあるため、1から説明します。

2.2.1. 必要なパッケージをインストールする

1. pythonのインストール

ここでは、python3.7を用いた。OSはWindowsを使用。

2. flirimageextractorのインストール

pip install flirimageextractor

にて、flirimageextractorをインストールする

pypi.org

3. その他、コードを実行しながら、必要なパッケージをインストールする

3章で示すコマンドにて、必要なパッケージを適宜インストールしてください。

2.2.2. この記事で用いたanaconda環境をそのまま自分のPCに複製する

さきほど述べたように、以下のレポジトリをダウンロード、または、クローンし、envフォルダの中にenv.ymlが存在していることを確認します。

github.com

以下のページにあるように、

conda env create -n 新たな環境名 -f ファイル名.yml

で、環境の複製が可能です。

qiita.com

今回の場合は、env.ymlが存在しているフォルダに移動し、

conda env create -n myEnv -f env.yml

を実行することで環境の複製を行うことができます。

3. メインコードの実行

3.1. exiftoolのパスの設定

demo.pyの35行目周辺に以下のコードがあります。ご自身のexiftoolのパスに置き換えてください。Dドライブではなく、Cドライブにexiftoolを置くほうがよいかもしれません。

exiftoolpath = "C:\Program Files (x86)\exif\exiftool.exe”

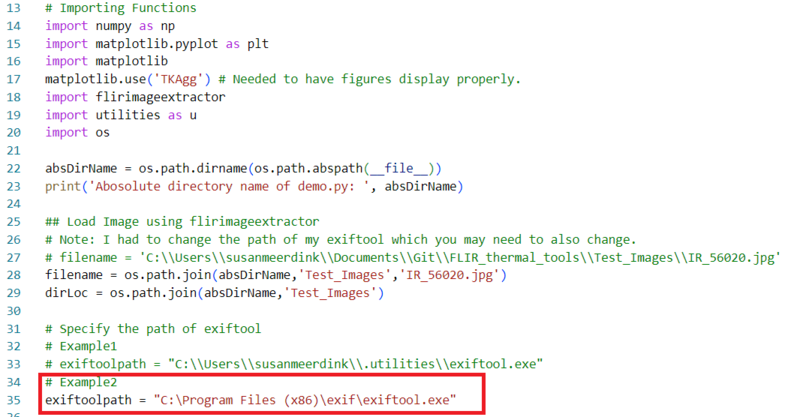
3.2. demo.pyの実行

demo.py や utilities.py のあるディレクトリで、demo.pyを実行すると、Test_Imagesフォルダ内の画像に対して、テストコードが実行されます。特に引数の設定は必要ありません。

私はAnaconda環境を用いているため、Anaconda Promptから実行しています。

このコードにより、熱画像からRGB画像およびCSVファイルの保存を行います。

また、以下のような画面が出てくれば、左の赤外線画像と右のRGB画像の順に、右クリックで、対応している点を選びます。できるだけ多くの対応点を選択し、エンターボタンを押してください。

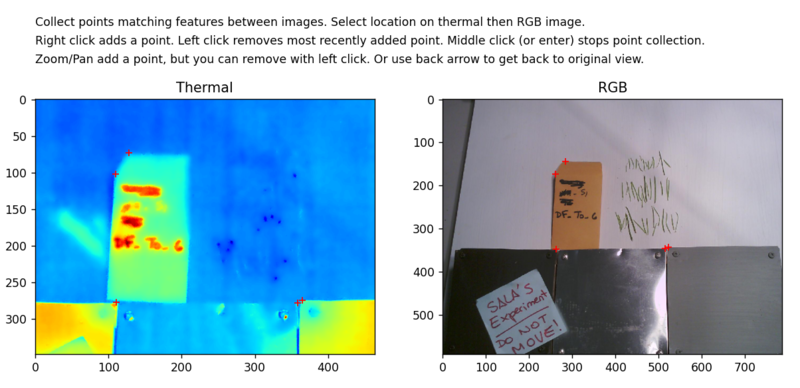
赤外線カメラの画像と、そのRGB画像には、ずれ（offset）があり、補正をする必要があります。上で述べた、exiftoolsをつかって、そのoffset値を読み取ることもできるのですが、必ずしもぴったりといくわけではなく、手動による補正が必要な場合もあるようです。

これにより、FLIR社製の赤外線カメラの画像をRGB画像に変換し、さらに、その温度情報をCSVファイルに書き込むことができます。

4. まとめ

この記事では、Pythonを用いて、FLIRの赤外線カメラの画像からRGBおよび、温度情報を表す、CSVファイルを取得することができました。この方法を用いて、経時的に取得した大量の画像や、多視点からの画像を自動的に処理できそうです。

2022-08-20

voxelPlotterを利用して、点群とグリッドを重ね合わせてみよう

3次元点群 matlab

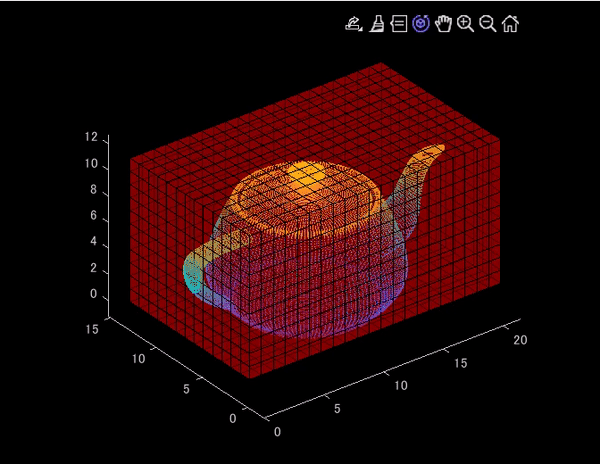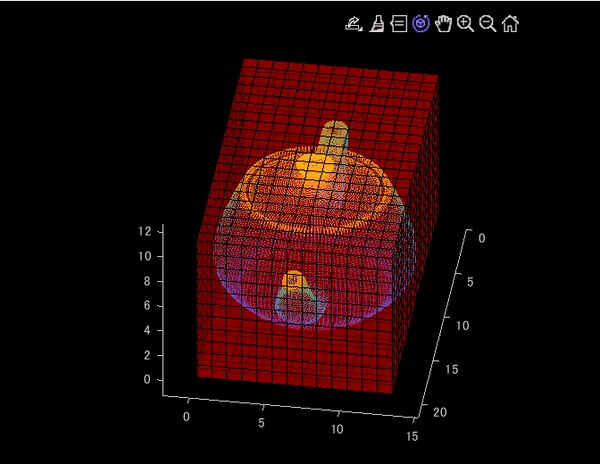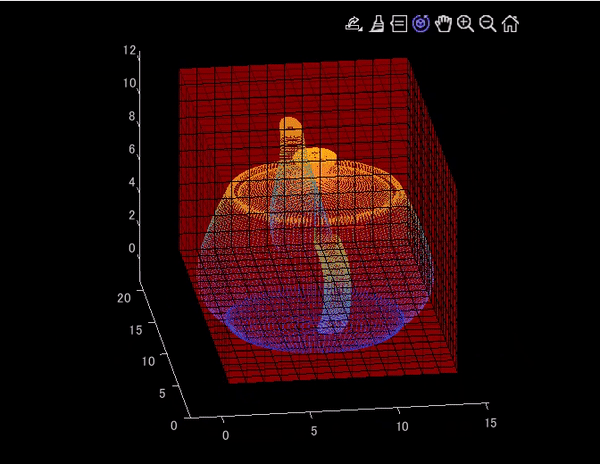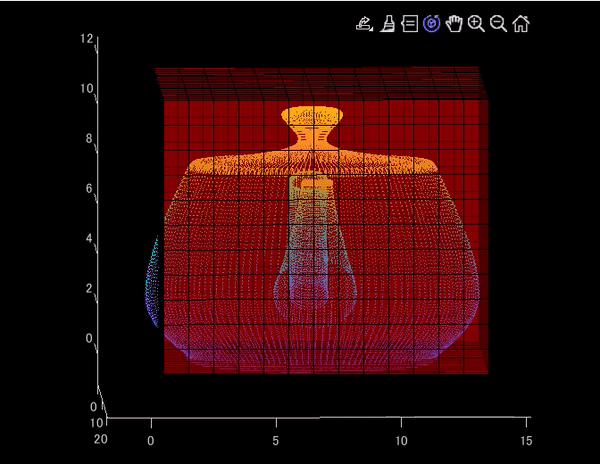
この記事では、以下のように、3次元点群にグリッドを重ね合わせて表示する方法について紹介します。メインのコードである、VoxelPlotter.mは、以下のMATLAB Centralにて公開されているものを参考にしました。

jp.mathworks.com

メインコード

アイデアとしては、voxelPlotter.mの結果と、点群をスケールが合うように同時にプロットするということです。なお、voxelPlotter.mについても、グリッドの透明度を変えられるように微調整しています。この記事で用いられたコードは以下のページにアップロードされています。

github.com

clear;clc;close all

% グリッドサイズの設定。小さくするとよりたくさんグリッドが表示される
gridSize = 0.3;
% テストデータの読み込み
pt = pcread('teapot.ply');
% 最小値を用いて、原点方向にシフト
xyz = pt.Location-[pt.XLimits(1),pt.YLimits(1),pt.ZLimits(1)];
% 点群の変数を作成
pt_shifted = pointCloud(xyz);
% シフトしたあとの、座標の最大値を取得
xyzMax = [pt_shifted.XLimits(2),pt_shifted.YLimits(2),pt_shifted.ZLimits(2)];
% グリッドの作成
VoxelMat = ones(round(xyzMax./gridSize));
% 表示
figure('Visible','on')
% メインコード。3つめの引数で、グリッドの透明度を制御できる
[vol_handle]=VoxelPlotter(VoxelMat,1,0.3);hold on;
pcshow(pt_shifted.Location./gridSize)

2022-08-17

argparseの使い方についてのメモ：Python編

python

前回のMATLAB編に続き、Python編です。こちらのPython編では、簡単な例にとどめます。

MATLAB編は以下のリンクからアクセスできます。

kentapt.hatenablog.com

今回のPythonコードは以下に保存されています。

github.com

argparseを用いた簡単なPythonコードの例

基本的な考え方や書き方はMATLAB編と同じで、コマンドの例が微妙に異なります。

# import module
import argparse

# argparseの中身の定義
parser = argparse.ArgumentParser()
parser.add_argument('firstArg1', type=float) # float, stringなどの変数の型を指定できる
parser.add_argument('--input_path', type=str, default='None', help='input path')
parser.add_argument('--value1', type=float, default=0.5, help='label path')
parser.add_argument('-a','--long_name', type=str, default='None', help='abbreviation')
# argsに、引数の値が格納される
args = parser.parse_args()

# パラメーターの確認
print('firstArg1 = '+str(args.firstArg1))
print('input_path = '+args.input_path)
print('value1 = '+str(args.value1))
print('long_name = '+args.long_name) # 省略後ではなく、正式名で参照する

コマンドの例

以下のようにコマンドを実行します。

1つ目の10という値がコード上のfirstArg1に相当します。
--input_pathの後にパスを指定できます。
--value1はdefaultの値が指定されている（0.5）ので、指定しない場合はvalue1=0.5になります。
-aといった書き方で、省略形を定義できます。

python argparsePractice.py 10 --input_path D:\blog -a abbreviation

入力引数について確認したい場合は、--helpや-hと打てばよいです。

python argparsePractice.py --help or python argparsePractice.py -h

参考ページ

qiita.com

2022-08-16

argparseの使い方についてのメモ：MATLAB編

MATLABであれば、livescript、Pythonであれば jupyternotebook (lab)といった、対話型の開発環境を筆者は使うことが多いのですが、コマンドラインで、引数を指定して実行できるようにする機会も多くあります。そこで、MATLABやPythonで、そのような指定（argparse）を使うときのメモを残します。

また、少し違う書き方もできて、そちらのほうが便利かもしれません。本記事のほかに以下のような方法もあります。

qiita.com

なお、本記事のコードやデータは以下のページに保存されています。

github.com

argparseの例

ここでは、以下のMATLABのセクションで用いる処理を例に説明します。findCat.mというMATLAB関数を作成し、それをコマンドライン（MATLABの場合は、コマンドウィンドウ）で実行することを考えます。ここで使うコマンドの例は以下の通りです。

findCat('./testImage/cat.jpg');
findCat('./testImage/cat.jpg',5);
findCat('./testImage/cat.jpg',10,'Opacity',0.1,'shape','circle');

ここで、以下のように、入力の画像だけを指定して実行してみます。

findCat('./testImage/cat.jpg');

以下の動画のように、ウィンドウが表示されて、何かを囲むように指示されます。例えば、猫の顔を囲んでみましょう。薄く、指定した範囲が黄色で囲まれたことがわかります。

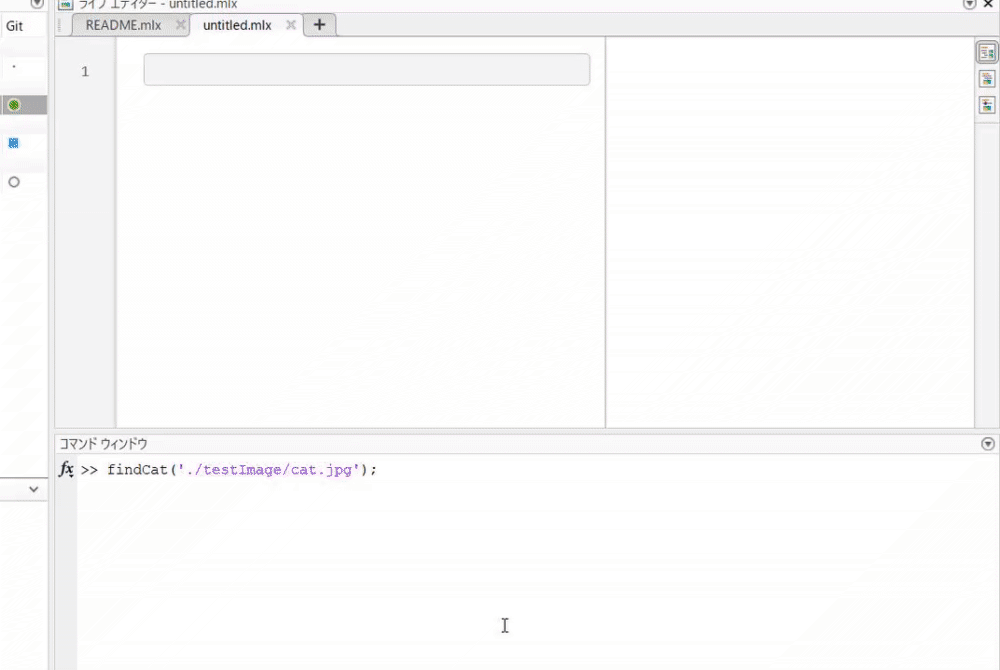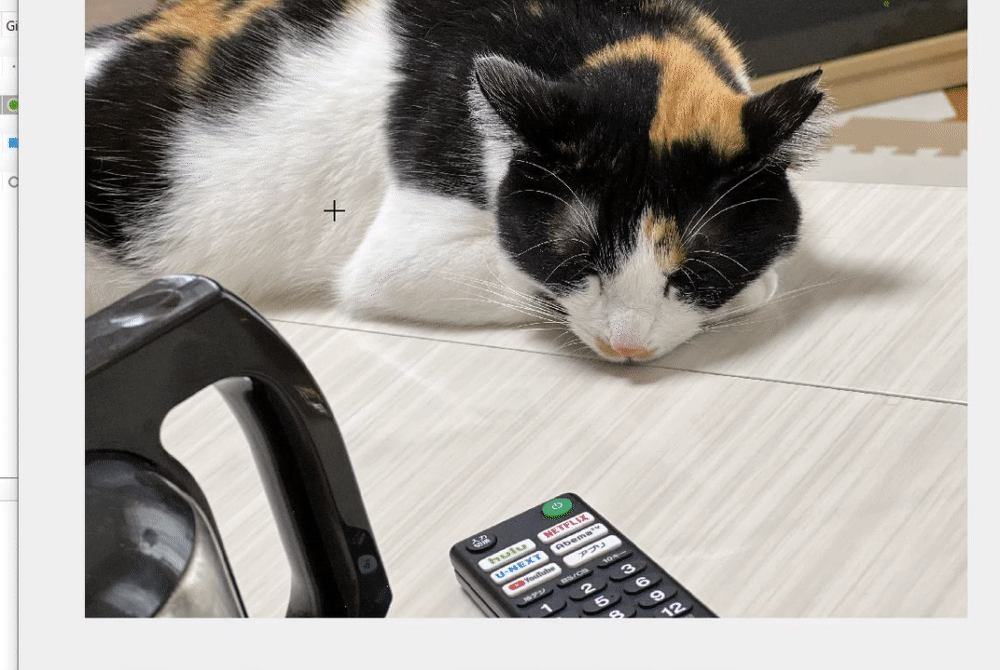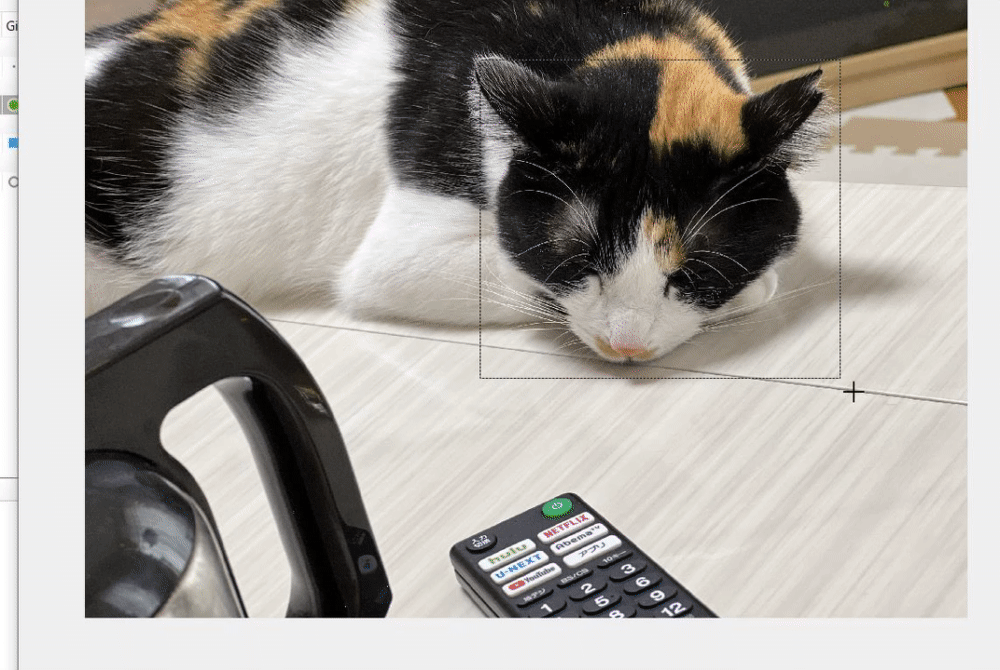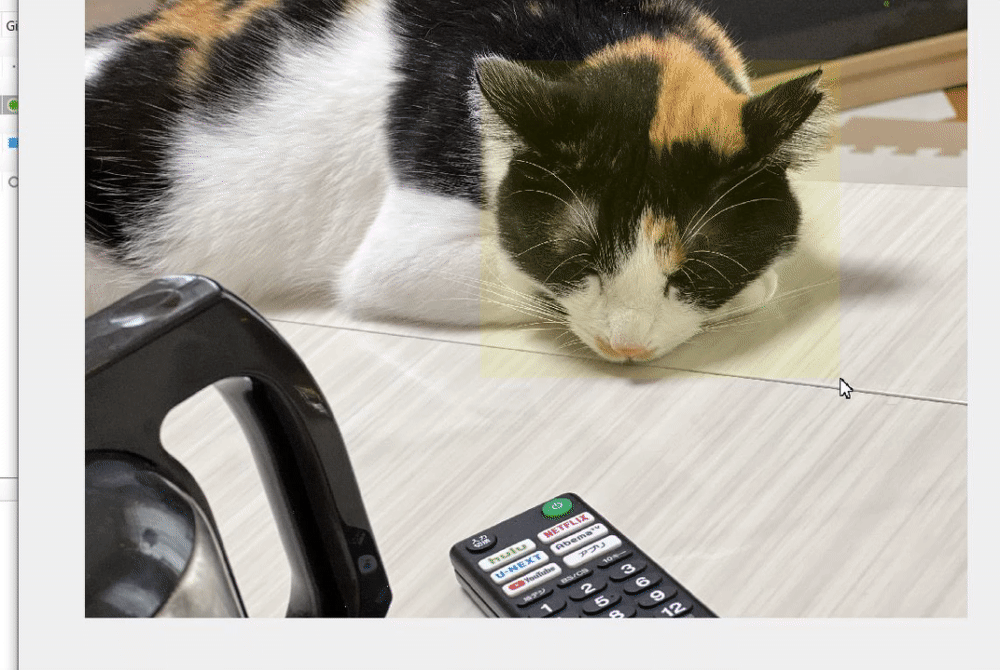
次は、以下のコマンドを実行してみます。

findCat('./testImage/cat.jpg',10,'Opacity',0.1,'shape','circle');

指定された範囲が、丸で囲まれました。

次に、cat.jpgのあとの値を大きくしてみます。

findCat('./testImage/cat.jpg',40,'Opacity',0.1,'shape','circle');

円の枠線が太くなりました。どうやら、この値を大きくすると、枠線が太くなるようです。

次は、shapeの後の値をfilledRectangleに変更してみます。次は、中身が色塗りされた長方形で囲まれました。

findCat('./testImage/cat.jpg',1,'Opacity',0.1,'shape','filledRectangle');

最後に、Opacityの値を0.8にしてみます。

findCat('./testImage/cat.jpg',1,'Opacity',0.8,'shape','filledRectangle');

透明度が下がり、より濃い黄色の長方形が作成されました。

argparseを試してみた結果

このように、コマンドラインの引数を変えることで、挿入する図形の形状を変更をしたり、幅や透明度をカスタマイズすることができました。コードの中身そのものを変えるのではなく、コマンドで変えるだけなので、運用も簡単になりそうです。

argparseについてもう少し詳しく

以下のコマンドをもう一度見てみます。10という値は、画像のパスの後に来ていて、特にどういうパラメーターなのかは、コマンド上では明示していません。一方、Opacityや、shapeといったパラメーターを宣言してから引数を入力する部分も確認できます。前者のほうは、特にパラメーターを宣言する必要がないので、コマンドがシンプルになります。調整するパラメーターが少ない場合は、便利ですが、パラメーターの数が多いと、非常にたくさん値が並び、混乱を招きます。'Opacity'などと宣言する場合は、これらを書く手間はありますが、どのパラメータを調整しているのかわかりやすいです。

findCat('./testImage/cat.jpg',10,'Opacity',0.1,'shape','circle');

コーディングについて

おおまかには以下のようなステップで進みます。コード中にコメントを入れていて、今後は、これをフォーマットとしてコピーアンドペーストし、変数の名前などを変えていくとよいでしょう。

1 各パラメーターのデフォルトの値の設定 2 inputParser変数の作成 3 パラメーターの定義 4 各パラメーターの値の読み取り

function imgOut = findCat(img,varargin)
   % デフォルト（既定）の値の設定
   defaultOpacity = 0.1;
   defaultLineWidth = 5;
   defaultShape = 'rectangle';
   % 選択肢を設定することもできる
   expectedShapes = {'circle','rectangle','FilledRectangle'};
   
   % inputParser変数の作成
   p = inputParser;
   % 変数が数値であり、かつ0より大きいことを確認する関数を定義する
   validScalarPosNum = @(x) isnumeric(x) && isscalar(x) && (x > 0);
   % 画像のパス @ischarにて、文字型であることを確認する
   addRequired(p,'img',@ischar);
   addOptional(p,'LineWidth',defaultLineWidth,validScalarPosNum);
   addParameter(p,'Opacity',defaultOpacity,validScalarPosNum);
   addParameter(p,'shape',defaultShape,@(x) any(validatestring(x,expectedShapes)));
   parse(p,img,varargin{:});
   % 各パラメーターを変数に格納する
   img = p.Results.img;
   LineWidth = p.Results.LineWidth;
   Opacity = p.Results.Opacity;
   ShapeName = p.Results.shape;
   
   % 画像の読み込みと表示
   I = imread(img);
   figure;imshow(I)
   % 図の上で囲む範囲を指定する
   rect = getrect();
   title('図の上で囲む範囲を指定してください')
   
   % 挿入する図形の種類に応じて、処理をスイッチする
   switch ShapeName
       case 'circle'
           % 描く円の中心と半径を定義する
           centroid = [rect(1)+rect(3)/2,rect(2)+rect(4)/2,rect(3)/2];
           % 円の挿入
           imgOut = insertShape(I,'Circle',centroid,'Opacity',Opacity,'LineWidth',LineWidth);
       case 'rectangle'
           % 長方形の挿入
           imgOut = insertShape(I,'FilledRectangle',rect,'Opacity',Opacity,'LineWidth',LineWidth);
       otherwise
           % 色が塗られた長方形の挿入
           print('FilledRectangle')
           imgOut = insertShape(I,'FilledRectangle',rect,'Opacity',Opacity,'LineWidth',LineWidth);
   end

   %イメージを表示
   figure;imshow(imgOut);

end

1 はじめに

2 決定係数の求め方について

2.1. 偏差積和を用いた傾きと切片の式の展開

2.1.1. 傾きについて

2.1.2. 切片について

2.2. 平方和の分解

2.3. 決定係数の式の定義

2.4. 決定係数と相関係数rの関係

3. MATLABとExcelを用いて、2章の決定係数の式が正しいか確認してみよう

3.1. MATLABのregress関数にて、単回帰分析を行った場合の決定係数の値

3.2. Excelにて、単回帰分析を行った場合の決定係数の値

3.3. MATLABにて2章の結果を1から書いて計算させたときの決定係数の値

4. 簡単なまとめ

5. 参考文献（本文中に記載のないもの）

1 はじめに

2 解析方法

3 導出

3.1. aとbについて偏微分

3.2. 正規方程式を解く

4. コーディングをもとに検算

4.1. MATLABのregress関数にて、単回帰分析を行った場合の傾きと切片の値

4.2 Excelにて、単回帰分析を行った場合の傾きと切片の値

4.3 MATLABにて3章の結果を1から書いて計算させたときの、傾きと切片の値

5. 行列を用いて解いた場合

6. 単回帰分析の性質の例

6.1 推定された回帰直線は、サンプルのxとyの平均を通る

6.2 回帰残差の和はゼロとなる

6.3 回帰残差とxの値はベクトルとして直交している

7. 疑問点：線形回帰と主成分分析では何が異なるのか

8. その他：ガウスとルジャンドルとの論争

9. 簡単なまとめ

10. 参考文献（本文中に記載のないもの）

点群ファイルの読み込み

座標系の変換

projcrsオブジェクトの作成

経度・緯度への変換

3次元マップでの点群の可視化

まとめ

参考にしたページ（本文中に記載がないもの）

1. はじめに

2. 環境構築について

2.1. Exif toolのダウンロード

2.2. Pythonの実行環境について

2.2.1. 必要なパッケージをインストールする

2.2.2. この記事で用いたanaconda環境をそのまま自分のPCに複製する

3. メインコードの実行

3.1. exiftoolのパスの設定

3.2. demo.pyの実行

4. まとめ

メインコード

argparseを用いた簡単なPythonコードの例

コマンドの例

参考ページ

argparseの例

argparseを試してみた結果

argparseについてもう少し詳しく

コーディングについて

2.4. 決定係数 $R^2$ と相関係数rの関係