MATLABでVelodyne LiDARのデータを可視化してみよう
この記事はMATLAB/Simulink Advent Calendar 2023の15日目の記事として書かれています。
また、本記事のスクリプトなどは以下のページにアップロードされています。
はじめに
LiDAR(Light Detection and Ranging)は、主にレーザー光線を物体に照射することで対象までの距離を測定します。それにより、周辺の障害物を検知したり、その環境の3次元的な地図を作成したりすることができます。
LiDARは多くの種類がありますが、その中でもVelodyne LiDARが有名です。本記事では、Velodyne LiDARのパケットキャプチャ(pcap)ファイルを再生し、3次元点群データを可視化する方法について紹介します。
MATLABにてVelodyne LiDARのデータを可視化した時の様子を示します。MATLABを利用すれば、特別なセットアップも必要なく、簡単に可視化することができます。
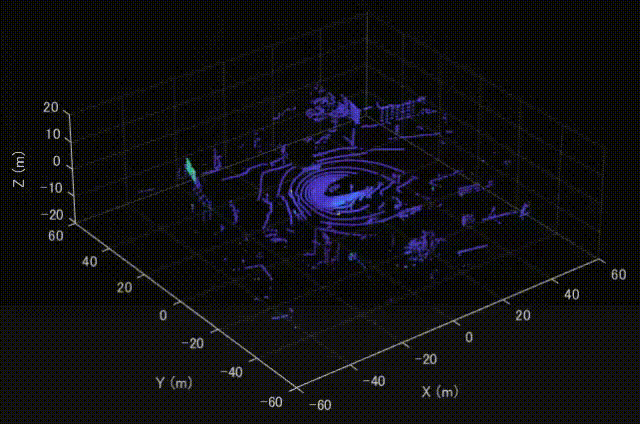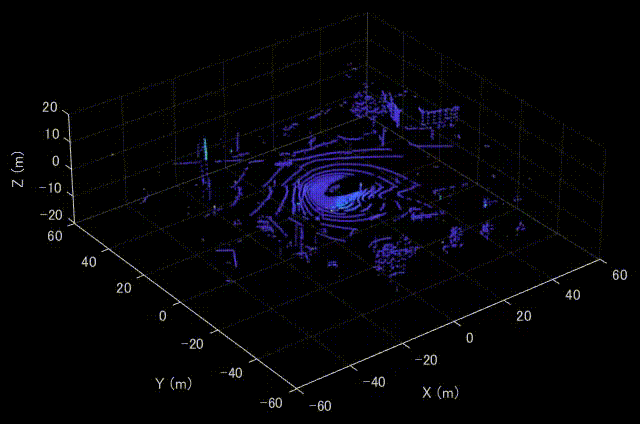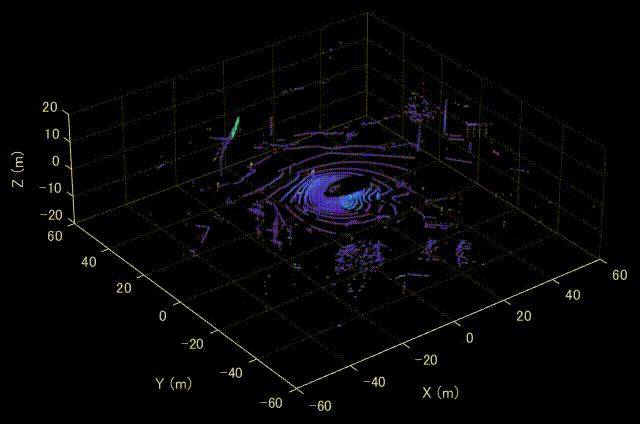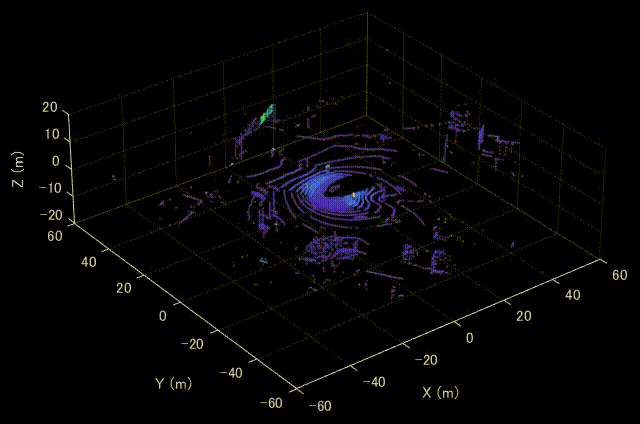
Velodyne HDL32Eについて
以下にVelodyne HDL32Eの画像を掲載します。

また、塩沢ら(2013)にてまとめられたVelodyne HDL32Eの性能について以下に掲載します。
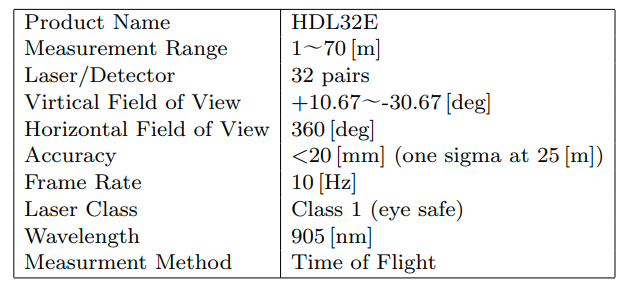
塩沢ら(2013): Velodyne レーザスキャナを用いた上空からの三次元再構成
その他のLiDARについてや、LiDARの利活用の例などについて以下のページがわかりやすかったです。
MATLABを利用したVelodyne HDL32Eデータの可視化
点群の可視化について
- pcplayer を利用して、時系列の点群データを再生することができます。
- xlimitsなどを定義することで可視化する点群の範囲を指定できます。
点群の読み取りについて
- velodyneFileReader を利用することで、Velodyne LiDARのデータを読み取ることができます。
- ここでは、HDL32Eという機種名を設定しました。
- readFrame 関数で1つずつ点群を読み取っていきます。
フレームごとの表示ついて
- view 関数で、さきほど定義したpcplayerを入力し、さらにそのプレイヤー上で見せる点群のXYZ情報や色付けするときのベースとなる反射強度(intensity)の情報を入力します。
まとめると以下のようになります。
clear;clc;close all % Velodyne Lidarデータの読み取りと可視化のためのMATLABコード % Velodyneファイルリーダーの作成 veloReader = velodyneFileReader('lidarData_ConstructionRoad.pcap','HDL32E'); % 可視化のための座標軸範囲の設定 xlimits = [-60 60]; ylimits = [-60 60]; zlimits = [-20 20]; % 点群データの可視化用のプレイヤーオブジェクトの作成 player = pcplayer(xlimits,ylimits,zlimits); % 座標軸ラベルの設定 xlabel(player.Axes,'X (m)'); ylabel(player.Axes,'Y (m)'); zlabel(player.Axes,'Z (m)'); % フレームごとにVelodyneデータを読み取り、可視化 for frameNumber = 1:veloReader.NumberOfFrames % フレームごとの点群データの読み取り ptCloudObj = readFrame(veloReader, frameNumber); % 点群データの可視化 view(player, ptCloudObj.Location, ptCloudObj.Intensity); % 表示の更新と一時停止(0.1秒) pause(0.1); end

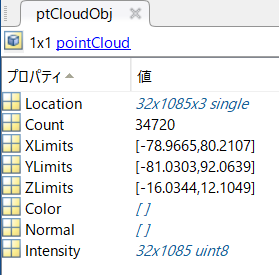
pointCloudオブジェクトの中身について
ここで、上で読み取った点群のフレームについてもう少し見てみます。
読みっとった点群はpointCloudオブジェクトとして読み取られます。
そこでは、点群を構成する点のXYZ情報(Location)や点の数(Count)、範囲(Limits)や色情報や法線ベクトルの情報、反射強度が格納されています。
Locationが以下の図では32×1085×3になっています。これは何でしょうか。
以下の図は、Velodyne VLP16の図です。16 beamsとあるように、
上下方向に16本のレーザービームがあり、それが高速に(10Hz)回転しています。
ここでは、Velodyne HDL32Eを利用しているため、32本のレーザービームごとに点が分かれていることを示しています。

それでは、32本のレーザービームを上から読み取って、可視化していきます。
% 新しいfigureを作成し、ライブスクリプトの外側で表示するように設定 figure('Visible','on'); % 1から32までのスキャンIDにわたるループ for scanId = 1:32 % ptCloudObjから指定されたスキャンIDに対応する点群データを取得 scan_i = ptCloudObj.Location(scanId,:,:); % 3D行列から2D行列に変換 scan_i = squeeze(scan_i); % 新たに点群を表示し、現在の点群を保持 pcshow(scan_i);hold on; % x、y、zの軸範囲を指定 xlim(xlimits); ylim(ylimits); zlim(zlimits) % 描画を更新 drawnow; end
実行すると、以下のように上側のスキャンから点群が可視化されていくことがわかります。
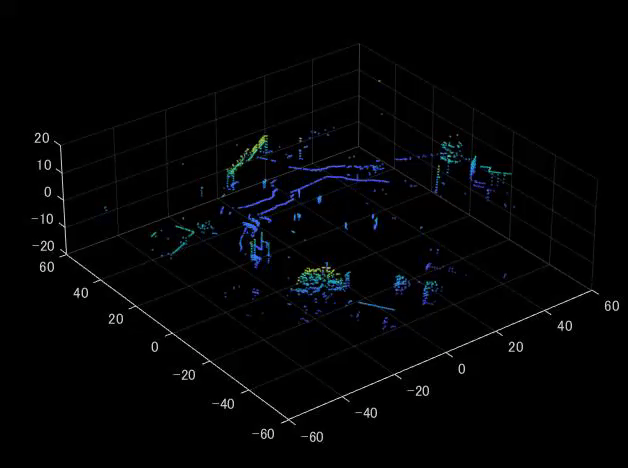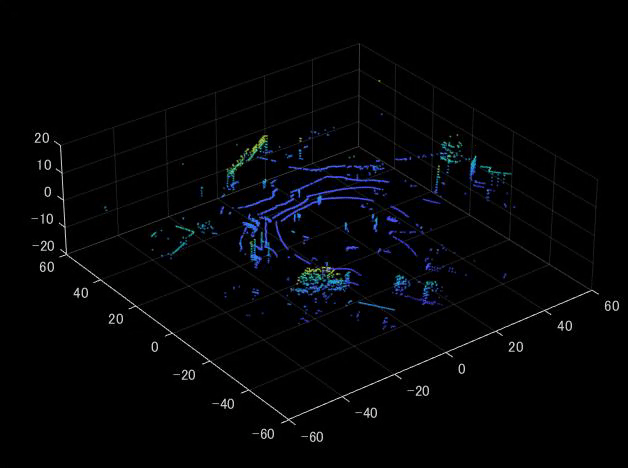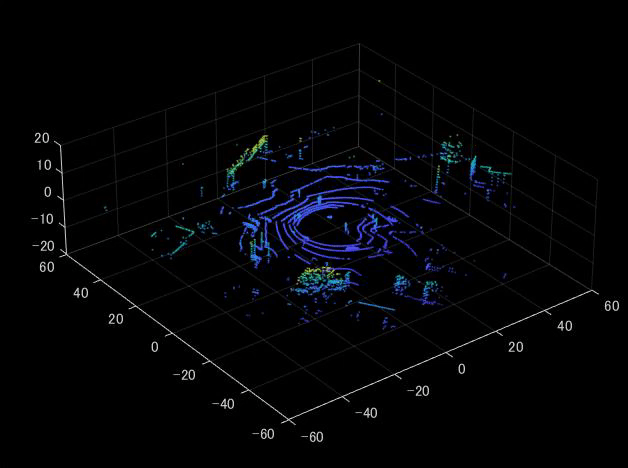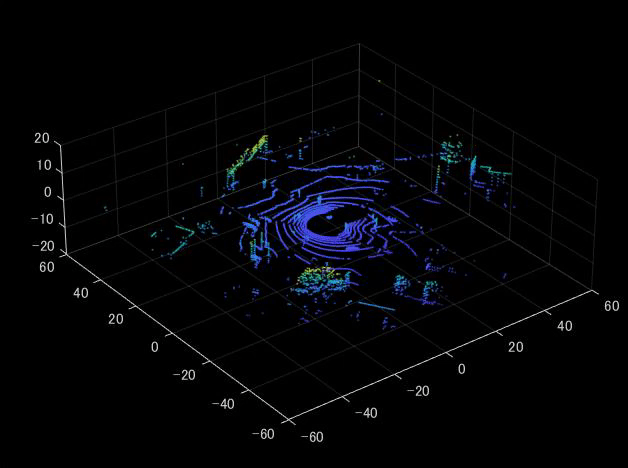
まとめ
この記事では、Velodyne LiDARのデータをMATLABを利用して可視化する方法について紹介しました。便利な関数が多く用意されており、特別なセットアップもなく、可視化ができました。
その他
この記事は、MATLABのライブスクリプトを利用して執筆されました。ライブスクリプトにてテキストや図、コードを書き、以下のコマンドで、マークダウン形式にエキスポートしています。
このマークダウン形式のデータをはてなブログにコピーアンドペーストすると効率よくブログ執筆を行うことができます。
export("visualizeHDL32E.mlx","README.md","EmbedImages",false)
参照座標系(EPSGコード)について
この記事はMATLAB/Simulink Advent Calendar 2023の16日目の記事として書かれています。
1. はじめに
3次元点群データは、XYZの点の集まりで表現されますが、「地球上での位置」を示すこともできます。
以下の図は、無料のGISソフトウェアであるQGISを利用して、地図上に3次元点群データを表示しています。
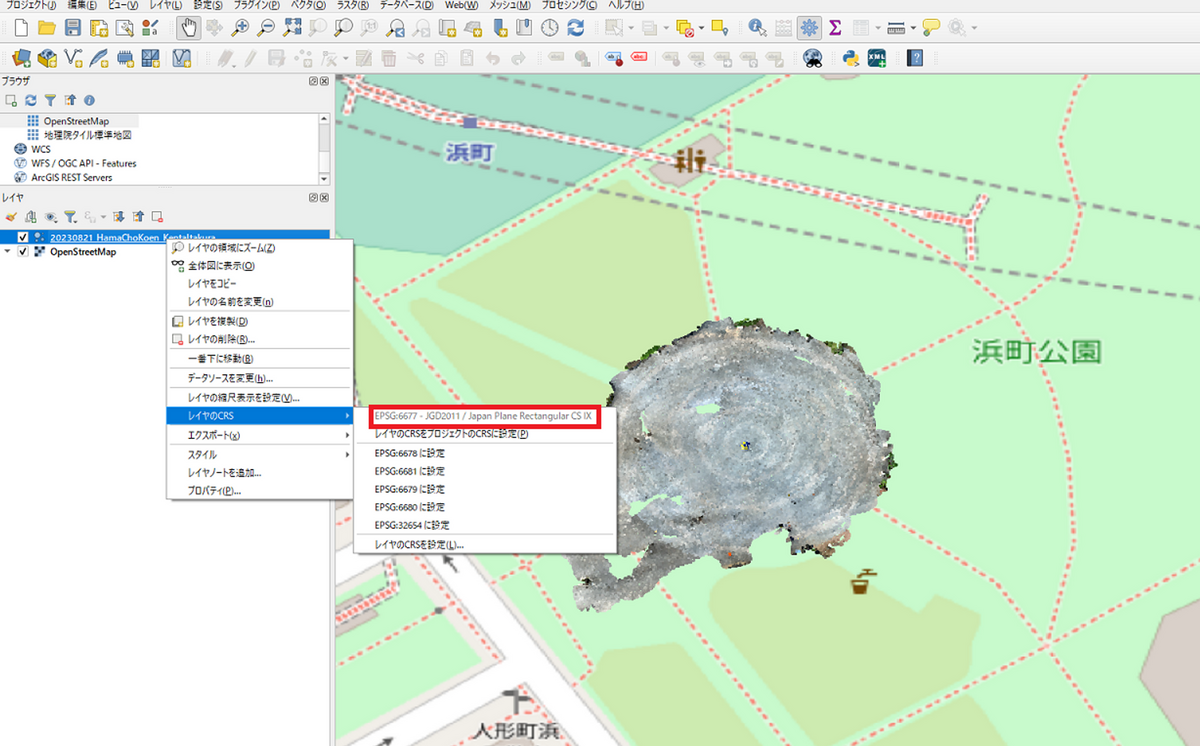
この際に、座標参照系(CRS)やEPSGコードというものを設定する必要があります。
この記事では、3次元点群データを地図上で見るために必要な座標参照系(CRS)やEPSGコードについてまとめます。
3次元点群データはiPhoneに搭載されたLiDARを利用して取得することもできます。
3次元点群データをiPhoneからエキスポートする様子については以下の記事をご覧ください。
2. EPSGコードについて
2.1. 地球上での点の位置を表す
取得した点群を地図上で表示させるためには、その点群が地球上のどこに位置するかを表す必要があります。以下の図のように、地球上の位置は、経度や緯度、高さの情報などを用いて表すことができます。以下の図では、きれいな楕円体の中での、位置を求めていますが、実際は、場所によって高低差があったり、複雑な地形をしていたり、単純に楕円体で地球を表すことは簡単ではありません。
また、シンプルかつ、地球の形状をうまく表現する楕円体を用意したのち、3次元的な地球(儀)で位置を表現するよりも、一部の領域であれば、2次元の平面に投影してしまっても実用上問題はありません。このように地球上での点群の位置を表すためにはいくつか方法があり、どのような方法をもとに表しているかを示す番号(のちに説明するEPSGコードに相当)があると便利そうです。地球上での位置を表す方法について、測地系と座標系に分けて説明します。
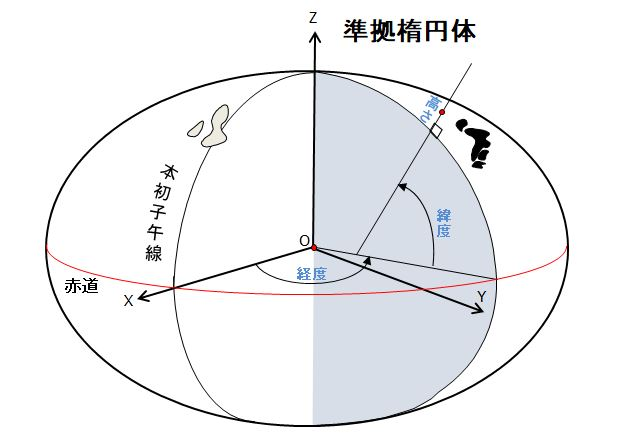
2.2. 測地系
測地系とは
- その経度・緯度の座標で表す時の座標の基準(点)
- 地球を楕円体とみなすときの形状
などを定義するための基準です。これにより、地図を作成する時や、測量時において、共通して地球上の位置を表現することができます。これにより、点群を正しく地図上で閲覧することができます。
測地系の中でも、世界測地系や局所測地系などが存在します。世界測地系は、国際的に定められた測地系です。一方、局所測地系は、その地域の近傍に対して適用できる測地系です。
局所測地系の例として、改正測量法の施行前は、明治時代に採用したベッセル楕円体という楕円体を地球を表すために用いていました。そして、これをもとにして、東京天文台の経度・緯度が、天文観測にて求められ、日本の原点の位置として決められました。
その後、VLBIや人工衛星などの技術の進歩により、より正確な地球の形状や大きさが求められるようになり、地球全体によく適合した測地基準系として、世界測地系が構築されました。
2.3. 座標系
地球上の点の座標を定める上で、測地系の他に、座標系について考える必要があります。座標参照系は大きく分けて、「地理座標系」「投影座標系」の2種類があります。この節では、この2種類の座標系について述べます。
2.3.1 地理座標系
地理座標系では、その点の位置を経度や緯度を用いて表します。
2.3.2 投影座標系
投影座標系では、一部の(限られた)範囲を2次元の平面へ投影する狭い範囲の一部を平面へ投影したときの座標を示します。ここでは、その投影した時の原点からのx方向およびy方向の値をもって、その点の位置を示すことができます。

投影の方法は複数存在し、以下の図のように
- 円筒図法
- 円錐図法
- 方位図法
といった投影方法が存在します。
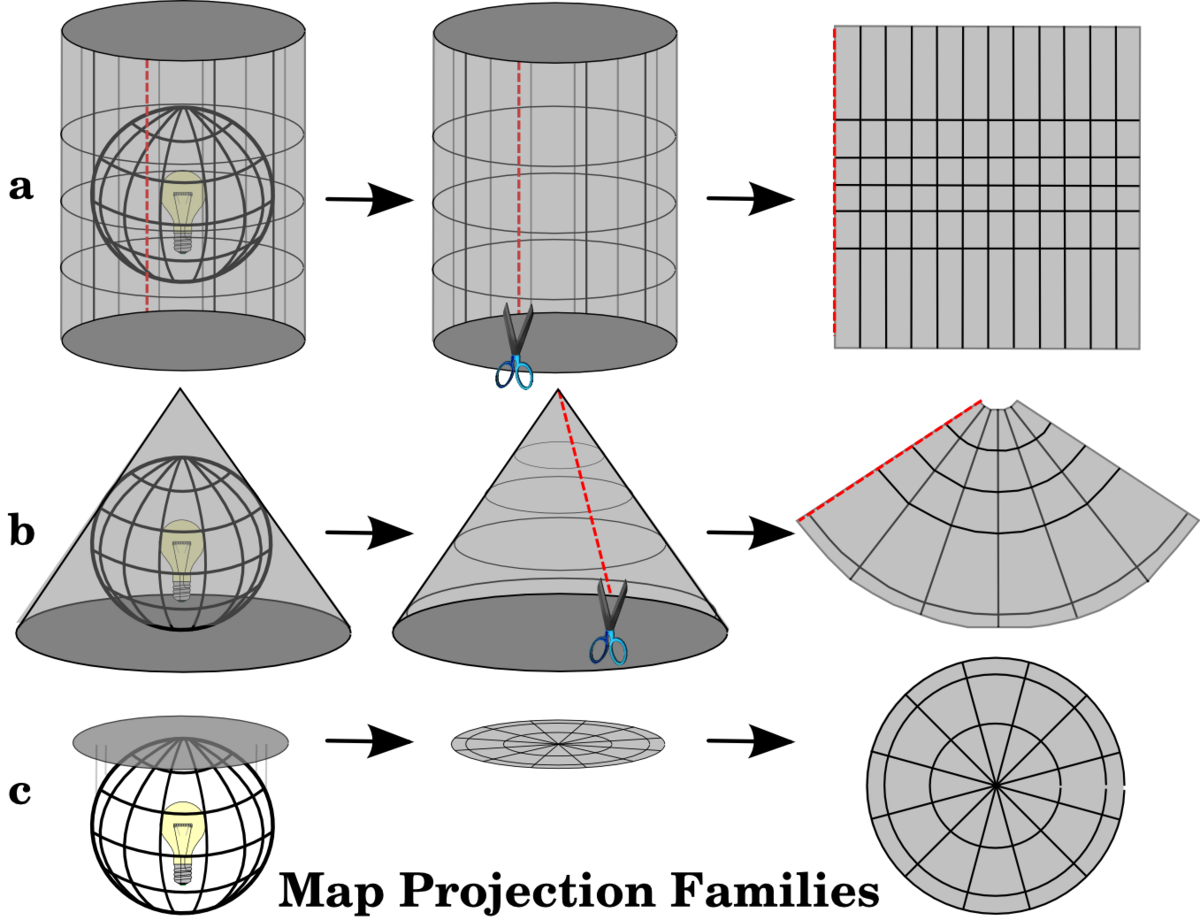
図出展: QGI documentation Coordinate Reference Systems ********(https://docs.qgis.org/2.8/en/docs/gentle_gis_introduction/coordinate_reference_systems.html)
2.4. 空間参照系
2.2で述べた測地系や2.3で述べた座標系の組み合わせによって、空間参照系を定義することができます。
測地系では、
- 地球を楕円体とみなした時の形状の詳細
- 楕円体とみなした時の原点
などが決められ、
座標系では、
- 経度や緯度を用いて表す
- 投影座標を用いて表す
- どのような投影方法を用いるのか
- どの場所を投影するときの原点とするのか
といったことが決められるのでした。
このような掛け合わせを経て、地球上の点の位置を定めるためのパターンは非常に多く存在します。そこで、空間参照系を識別するためのコードがあると便利です。

本図は、地図のワークブック 空間参照系(測地系/座標系/投影法)について (https://lonlat.info/spatialreferencesystem/) を参考に作成されました。
3. MATLABで点群の座標を経度・緯度に変換する
MATLABで点群の位置座標を変換してみます。データは、iPhone LiDARのアプリである、iPhone LiDARのアプリである、Scaniverseを利用して取得された点群を利用します。 主に、Mapping Toolboxを利用します。
以下のように対象の点群をMATLAB上でくるくると回すことができます。Scaniverseで取得された取得された点群をLAS形式でエキスポートした場合、UTM座標系が利用されます。

この点群のXYZ座標を読み取り、経度・緯度に変換したいと思います。
利用した点群データは以下にアップロードされています。ぜひダウンロードして、以下のコードを実行してみてください。
流れは以下の通りです。
- readPointCloud 関数を利用して点群の読み取り
- projcrs 関数を利用して、UTM54Nの projcrs オブジェクトを作成する
- projinv 関数を利用して、UTM54Nの座標を経度・緯度に変換する
- geoscatter 関数を利用して、地図上にプロット
clear;clc;close all % las/lazファイルを読み込むためのlasFileReader objectを作成する lasReader = lasFileReader('treeTrunk.laz'); % las/lazファイルの、xyzおよび色情報を読み込み ptCloud = readPointCloud(lasReader); % projcrsオブジェクトを作成する utm54N = projcrs(32654); % projinv 関数を利用して、UTM54Nの座標を経度・緯度に変換 [lat,lon] = projinv(utm54N,ptCloud.Location(:,1),ptCloud.Location(:,2)); % スムーズに可視化するため、点をサンプリング idx = randperm(ptCloud.Count,100000); % 色の取り出し ptCol = ptCloud.Color(idx,:); % 地図上にプロット geoscatter(lat(idx),lon(idx),1,single(ptCol)./2^16)
以下のようにプロットすることができました。軸ラベルを見ると、単位が、経度・緯度になっていることがわかります。

参考ページ
地図のワークブック 空間参照系(測地系/座標系/投影法)について
3次元点群の形式の1つであるE57ファイルについて
はじめに
この記事はMATLAB/Simulink Advent Calendar 2023の9日目の記事として書かれています。
LiDARなどにより取得される3次元点群ファイルの有名なフォーマットにe57があります。
e57は、XML データ形式に基づいて点群や各種データを階層ツリー構造で格納します。米国試験材料協会 (ASTM) によって定められています。
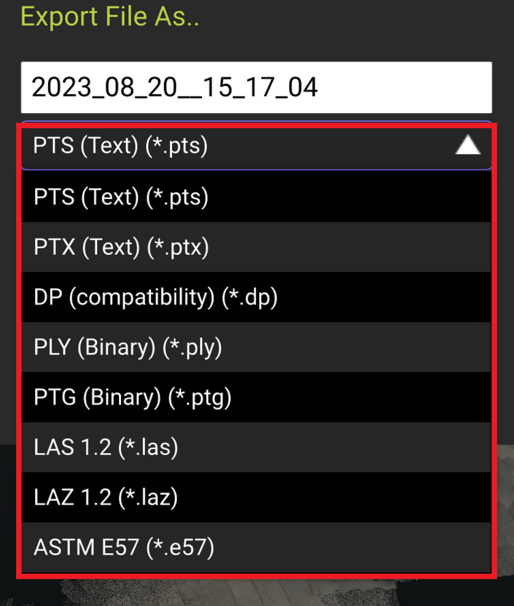
例えば、Leica社のCycloneで点群をエキスポートするときや、iPhone LiDARのアプリである、Dot3Dで点群をエキスポートするときにE57形式を選択することができます。
以下の図は、Dot3Dで点群をエキスポートするときの様子です。一番下にE57があることがわかります。
E57形式について
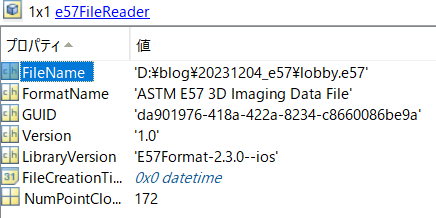
E57は、ヘッダー、バイナリーセクション、XMLセクションに分かれています。

画像出典:e57FileReader
https://jp.mathworks.com/help/lidar/ref/e57filereader.html
ヘッダーには、バージョン番号や、ファイルのフォーマットの名前などの情報が格納されています。
MATLABでE57形式の点群を読み込むと以下のようになります。
また、データ構造は以下のようになっています。Dota3Dという3次元的なデータと、Images2Dとあるような2次元的なデータに分かれています。高密度点群の標準的なフォーマットであるLAS形式の違いとして、スキャンごとの点群やその点群を取得した時の位置や姿勢、また、画像に関する情報が分かれていることが挙げられます。
LAS形式では、スキャンごとの点群は合成され、また、各点にRGBの色情報が投影された状態で保存されます。

画像出典:e57FileReader
https://jp.mathworks.com/help/lidar/ref/e57filereader.html
E57形式では、点群がスキャンごとに保存されるので、例えば以下のように2か所から計測した場合は、それぞれの点群とその時のスキャナの位置や向き、画像などが計測されます。
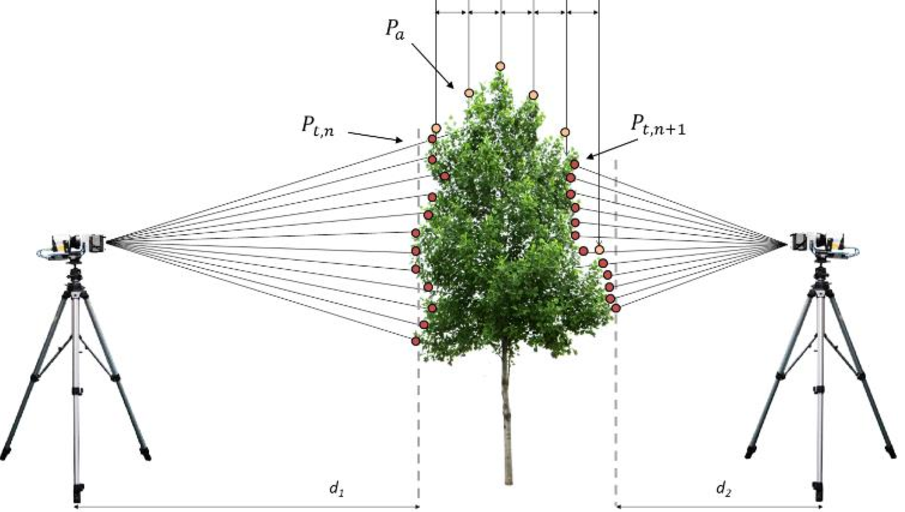
画像出典:Paris, C., Kelbe, D., Van Aardt, J., & Bruzzone, L. (2017). A novel automatic method for the fusion of ALS and TLS LiDAR data for robust assessment of tree crown structure. IEEE Transactions on Geoscience and Remote Sensing, 55(7), 3679-3693.
E57に関して、以下の記事がわかりやすかったです。
Interoperability around the E57 Scanning Format
https://www.cadinterop.com/en/formats/cloud-point/e57.html
姿勢情報について
E57形式ではスキャンが行われた時の位置や向きが格納されていると述べました。
MATLABでE57形式の点群を読み込み、さらに、Data3Dから姿勢情報を読み取りました。
また、点群とその姿勢情報(スキャンしたときのデバイスの位置と向き)を可視化しています。
表示における技術的な内容や、MATLABでのコーデイング方法については後述しています。
なお、このE57形式の点群は、iPhone LiDARのアプリである、Dot3Dを利用して取得されました。
Dot3Dを利用したスキャンの方法やエキスポートの方法については以下の記事をご覧ください。
デバイスの位置と向きはカメラのアイコンで示しています。iPhone LiDARのデータであるため
スキャンしたポイントが多く、たくさんのカメラのアイコンが表示されています。

近くで見ると、オレンジの枠で囲われた場所では、奥の自動販売機をスキャンしていて、
青色の場所では右側の自動販売機をスキャンしていることがわかります。

このように、それぞれスキャンされた点群とその位置や姿勢がわかるため、それらをつなぎ合わせることで、
1つの高密度な点群を合成することができます。
例えば、以下の画像では、3つのスキャンのみをランダムに取り出して、その姿勢情報を利用して変換することでうまくつなぎ合わせています。
赤色は自動販売機、青色は天井、緑はエレベーターをそれぞれスキャンしていることがわかります。
このような操作をE57形式の点群に含まれるすべての点群に対して繰り返すことで、スキャン全体の点群を得られます。

以下の動画は、iPhone LiDARにより取得された点群をスキャンごとに取り出し、さらにその時の位置とiPhoneの姿勢の情報を利用して重ね合わせています。
最終的に生成されたデータをアプリ上ではエキスポートすることができます。

回転と移動の行列について
E57ファイルには、スキャンした時のデバイスの位置や向きが格納されていますが、その表し方について説明します。
以下の図は2つのカメラの位置関係を示しています。この時、左のカメラの位置を基準として、右のカメラの位置を示すことを考えます。カメラを回転させる行列と平行移動させる行列があればそれを実現することができます。
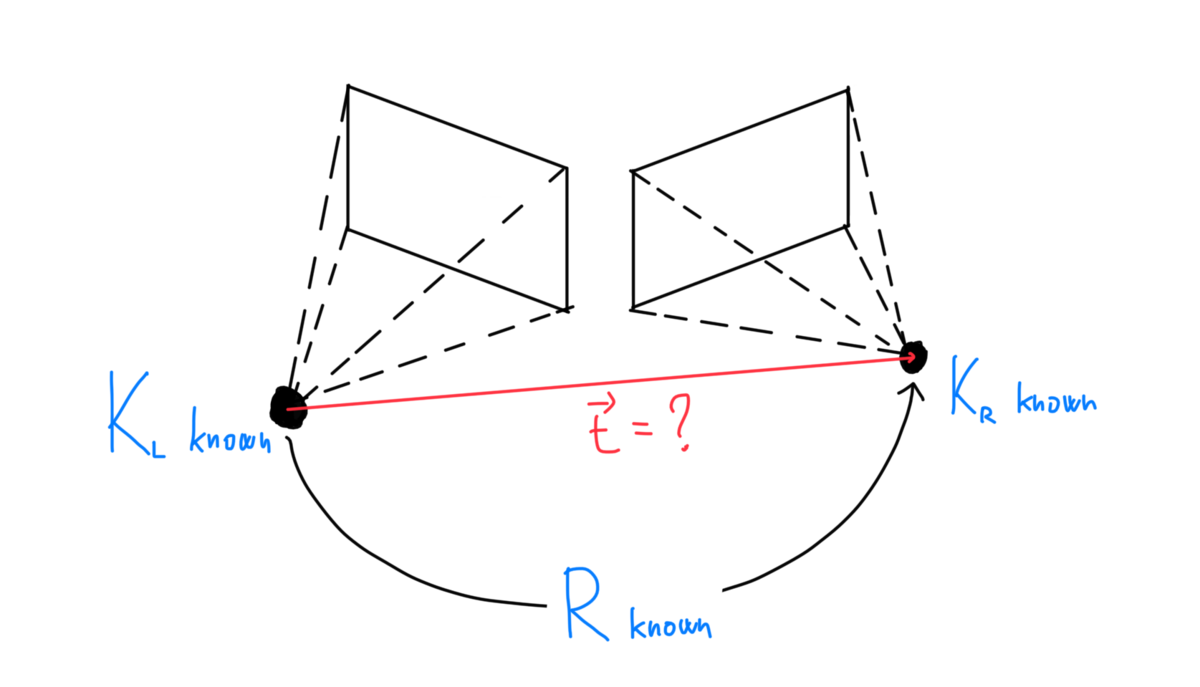
回転行列は3次元上で行うと3×3になり、平行移動は3×1です。それらを合わせると以下のような行列になります。
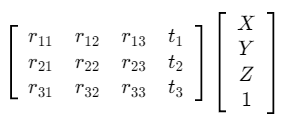
MATLABにて実践する
それでは、実際に上記の作業を行ってみます。
ポイントとして、以下のことが挙げられます。
- e57FileReader と readPointCloud で、E57形式の点群を読み込む
- pcMetadataにある、RelativePoseから姿勢情報の行列を取得する
- 行列の情報をもとに、点群を変換する
- 行列の情報をもとにデバイスの位置と向きを可視化する
また、ここでのサンプルファイルを以下に格納しています。適宜ダウンロードしてお使いください。
https://drive.google.com/file/d/1Ym1e2t5u6vcMlrsblqmGA3Q7RNi54mZp/view?usp=sharing
clear;clc;close all % e57ファイルから点群データを読み込むためのe57Readerオブジェクトを作成します。 e57Reader = e57FileReader("lobby.e57"); % 点群データ(ptCloudArr)および対応する姿勢(tformArr)を格納するための変数を初期化します。 ptCloudArr = []; tformArr = []; % 点群データを読み取ります。 for i = 1:e57Reader.NumPointClouds % e57ファイルからi番目のフレームの点群データ(ptCloud)とメタデータ(pcMetadata)を読み込みます。 [ptCloud, pcMetadata] = readPointCloud(e57Reader, i); % 各点群データと対応する姿勢をそれぞれの配列に追加します。 for j = 1:numel(ptCloud) ptCloudArr = [ptCloudArr ptCloud(j)]; tformArr = [tformArr pcMetadata.RelativePose]; % 相対姿勢を用いてカメラをプロットします。 cam = plotCamera(AbsolutePose=pcMetadata.RelativePose, Opacity=0, Size=0.1); hold on end end % 点群データと対応する姿勢を用いて点群の合成を行います。 pcMap = pcalign(ptCloudArr, tformArr); % 合成した点群を表示します。 figure;pcshow(pcMap)
補足
デバイスが3つだけ可視化された画像を作成するためのコードを示します。
ptCloudArr = []; tformArr = []; absTform = rigidtform3d; % 点群データを読み取ります。 figure; indices = [1 100 170]; colorList = {"red","blue","green"}; for ii = 1:3 i = indices(ii); [ptCloud,pcMetadata] = readPointCloud(e57Reader,i); for j = 1:numel(ptCloud) ptCloudArr = [ptCloudArr ptCloud(j)]; tformArr = [tformArr pcMetadata.RelativePose]; color_i = colorList{ii}; cam = plotCamera(AbsolutePose=pcMetadata.RelativePose,Opacity=0,Size=0.1,Color=color_i);hold on end end pcMap = pcalign(ptCloudArr,tformArr); pcshow(pcMap)

SOLOv2を利用した猫のセグメンテーション
はじめに
この記事はMATLAB/Simulink Advent Calendar 2023の2日目の記事として書かれています。
SOLOv2とは
画像中の物体ごとに色塗り(インスタンスセグメンテーション)をするネットワークです。
インスタンスセグメンテーションの有名な方法として、この他にMask R-CNNなどが知られています。
SOLOについては以下の記事がわかりやすかったです。
MATLABではSOLOv2モデルを非常に簡単に動かすことができます。

本記事ではSOLOv2を利用して以下のようなセグメンテーション結果を得る方法ついて説明します。また利用したコードや動画は以下のページに格納しています。
MATLABでSOLOv2を実行する
前準備:アドオンのインストール
はじめに、Computer Vision Toolbox Model for SOLOv2 Instance Segmentation をインストールしておく必要があります。
コードの実行
動画に対して、SOLOv2のモデルを実行し、猫の部分を色塗りしてみます。
ポイントは以下の通りです。
- solov2関数でSOLOv2モデルを読み込む
- segmentObjects関数で画像に対してSOLOv2を実行する
clear;clc;close all % solov2関数でSOLOv2モデルを読み込む net = solov2("resnet50-coco",InputSize=[800 800 3]); % 猫の動画を読み込む準備 catVideo = VideoReader("catVideo.mp4"); % 出力結果を保存する準備 v = VideoWriter('segmentationResult.avi','Motion JPEG AVI'); v.FrameRate = 10; open(v) % 猫を塗る色の指定 maskColors = "blue"; % ビデオから1フレームずつ読み取り、SOLOv2を実行 while hasFrame(catVideo) % フレームの読み込み frame = readFrame(catVideo); % フレームのリサイズ frame = imresize(frame,[800 800]); % SOLOv2の実行 [masks,labels,scores] = segmentObjects(net,frame,Threshold=0.2); % 猫のマスクの取り出し catMask = masks(:,:,labels=="cat"); % 猫のエリアの可視化 overlayedMasks = insertObjectMask(frame,catMask,MaskColor=maskColors,Opacity=0.3); % 画像の表示 imshow(overlayedMasks); % 動画への書き込み writeVideo(v,overlayedMasks) end close(v)
Cloud Compareを利用して点群を画像に変換してみよう
1. はじめに
この記事では、3次元点群の閲覧や処理の無料ソフトであるCloud Compare (クラウドコンペア: 以下CCとする)を利用して、点群を上から見た画像に変換する方法についてまとめます。設定方法によっては、オルソ画像やデジタル標高モデル(DEM)に相当するファイルをエキスポートすることができます。
CCのダウンロードリンクは以下の通りです。
また、本記事のより詳しい内容は以下のページをご参照ください。
本記事は、CCに点群をインポートする方法や閲覧する方法などはすでに把握しているとして進めます。
2. 変換する方法
2.1. アイコンのクリック
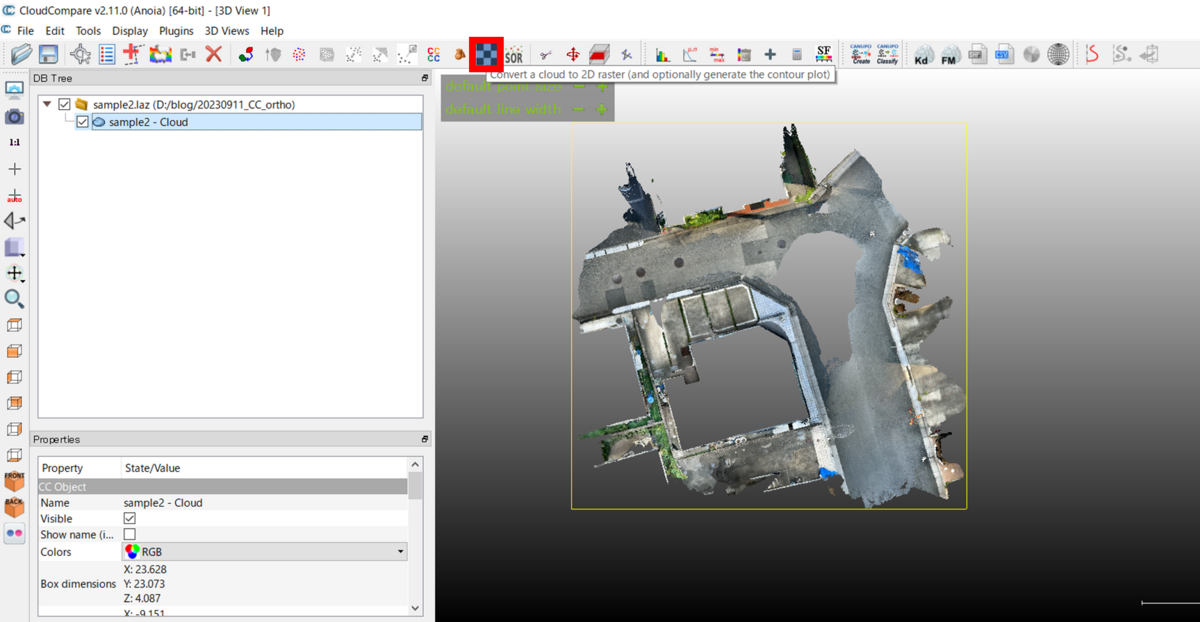
Convert a cloud to 2D raster を選択します。以下の赤枠をクリックしてください。
2.2. パラメータ設定
ここでは、簡単にパラメーター設定を行います。特に重要な値のみ本記事では記述いたします。
Gridについて
step: 2次元画像に変換した時の1ピクセル値の距離。この値を変えることで、sizeの値も変わる
size: 2次元画像に変換した時の画像サイズ。大きいほどファイルサイズも大きくなる
active layer: どの値を利用して2次元画像に変換するか。Height grid valuesでは、そのピクセルの位置の高さ(Zの値)を利用して変換する。他の値を利用して2次元画像に変換したい場合はこの値を変更する
Projectionについて
direction: どの向きに沿って2次元画像に変換するかどうか。例えば、Zを設定すると、ちょうど鉛直上向きから見たとき(上から下を見たとき)の2次元画像に変換する
cell height: 各グリッドのどの値を利用して、2次元画像に変換するかどうか。maximumの場合は、そのグリッドに位置する値の中で最大値を利用する。
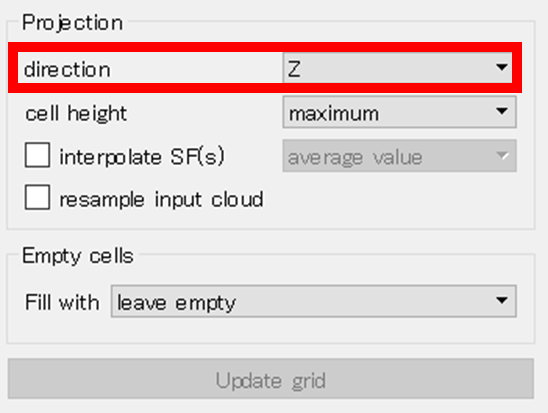
例えば、directionをXにすると、横から見たような画像になる。
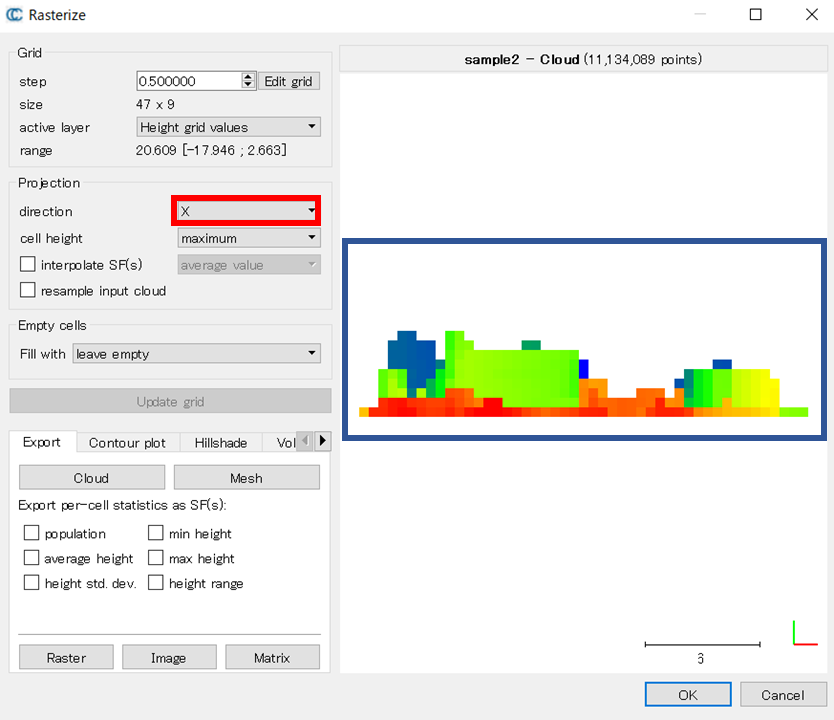
Empty cellsについて
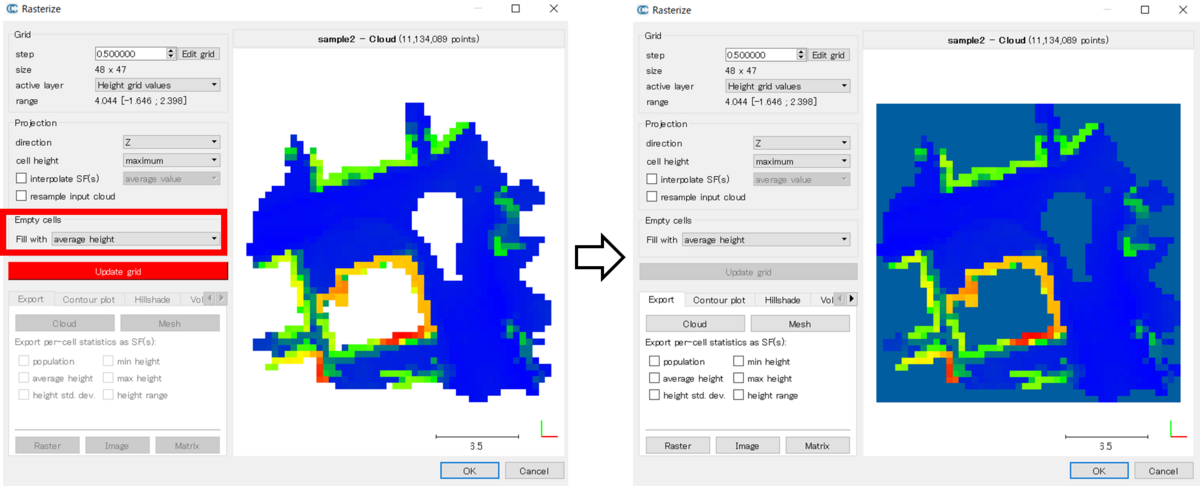
そのグリッドに相当する点が存在しないときに、どのような処理をするか。例えば、点群ファイルに大きな穴があると、それを上から見たときにその穴に相当する場所の値(例:Z値)は存在しない。その場合は、値がないとする、近くの値で補間する、といった処理を選択することができる。以下の画像のように、点群の真ん中に穴がある場合、白色になっていることがわかる。仮に、Empty cellsに処理を指定した場合、それに従ってそのグリッドの値を計算する。
2.3. 計算結果の更新
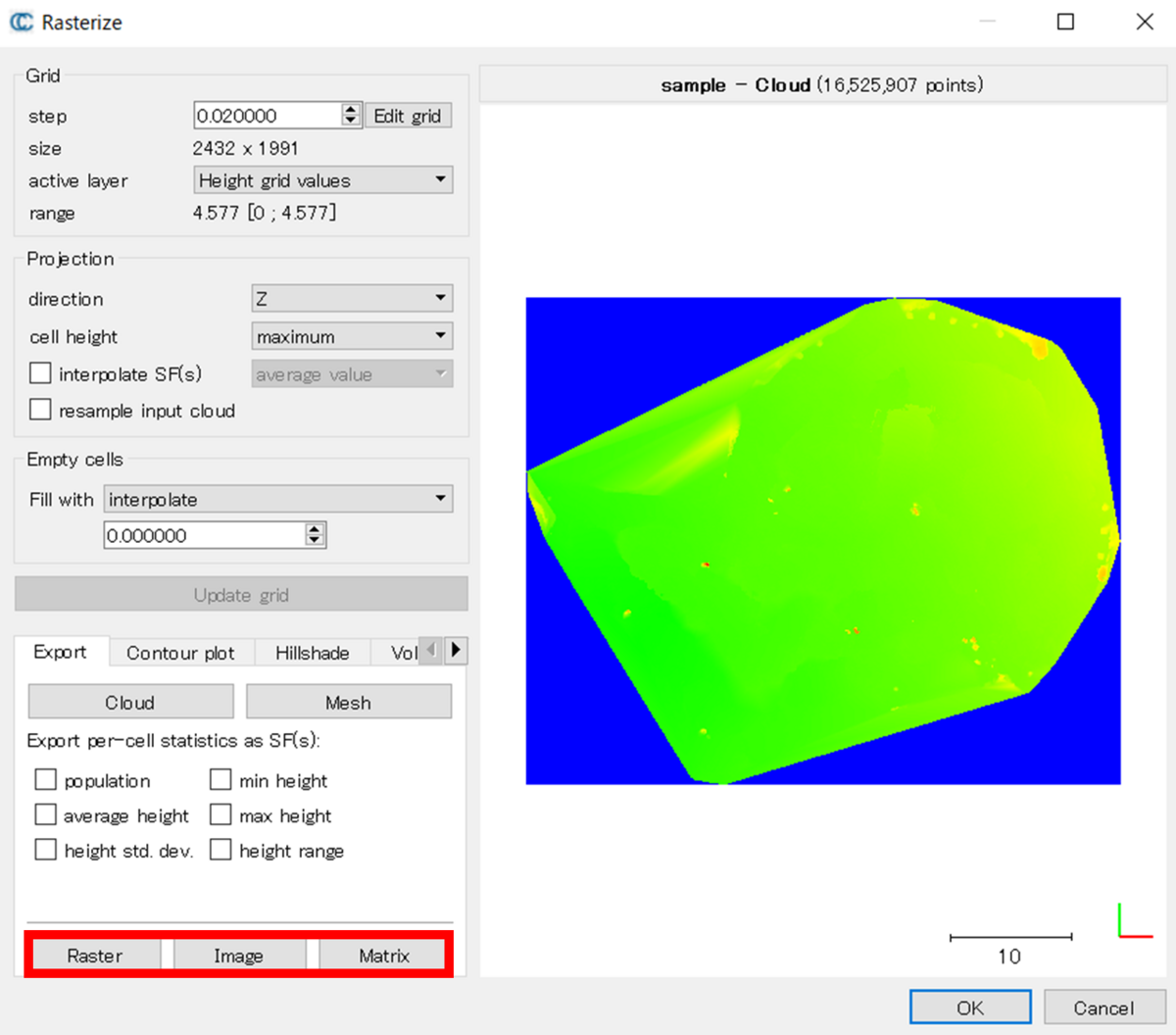
2.2のパラメーター設定を行うことで、投影した時の様子が決定します。初めは右側のパネルが空白ですが、赤色のボタンをクリックすることで、右側のパネルも更新されます。出力結果のイメージが表示されていることがわかります。

2.4. 結果の出力
以下の赤枠から計算結果を別ファイルとして保存することができます。
Raster: tif形式。GISソフトウェアなどで閲覧することができる。
Image: 画像形式。画像として保存できる。
Matrix: text形式。数値としてメモ帳などで確認できる。
3. 結果の確認
3.1. QGISでの読み込み
Raster形式で保存したファイルをQGISにて読み込みました。Empty cellsに関しては、特に処理を行っていません。点群を取得した位置で可視化されていることがわかります。

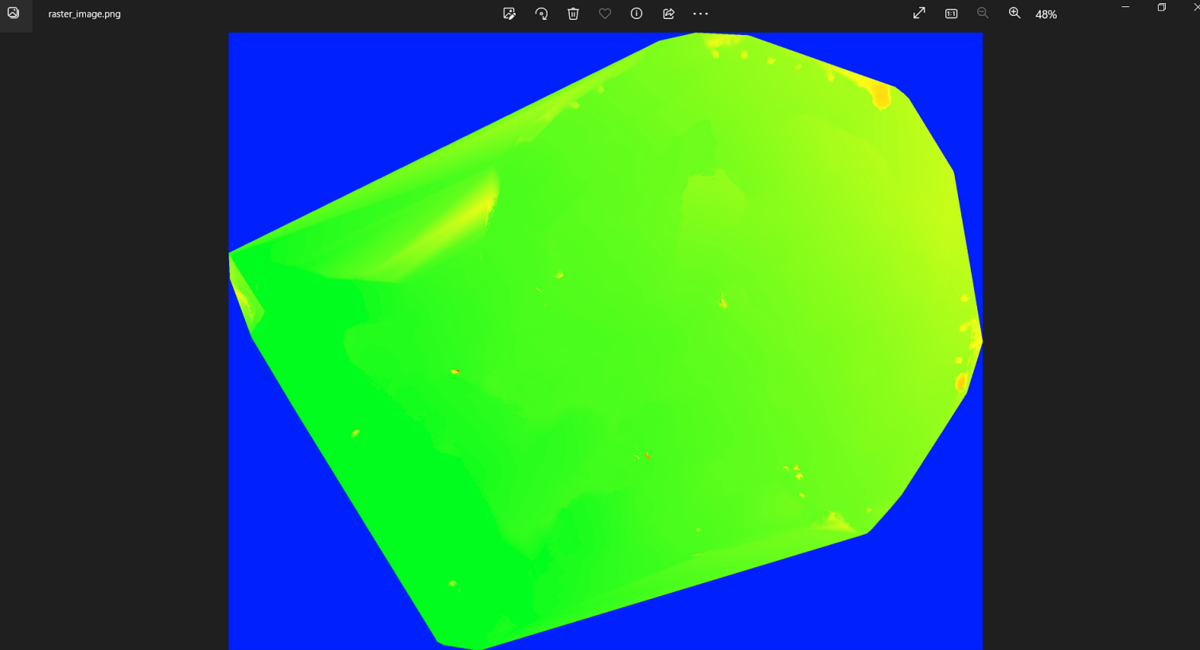
3.2. 画像の読み込み
Image形式でエキスポートした場合、png形式で画像が保存されました。報告書作成などに便利そうです。
3.3. Matrixでの読み込み
Matrixで保存した場合、以下のようにメモ帳で開くことができました。別の計算式などを別途実行したい場合やプログラミング言語を使って再処理したい場合などに便利そうです。

4. まとめ
本記事では、CCを利用して、点群から2次元画像に変換する方法について述べました。例えば、RGB情報を利用して投影すればオルソ画像になりますし、高さ情報を利用すれば、デジタル表層モデル(DSM)、また地表面の点のみを利用すればデジタル標高モデル(DEM)になると思います。設定を適切に変えることで、色々なデータに変換できて便利な機能でした。
iPhone LiDARとDot3Dを利用して、3Dスキャンを行う
1. はじめに
iPhoneに搭載されたLiDARを利用して3次元測量をするためのアプリは多く存在します。この記事では、DotProduct社の提供するDot3Dの使い方について簡単にまとめたいと思います。Dot3Dは以下のAppストアのページからダウンロード可能です。
なお、本記事においては、iPhone 13Pro Maxを利用しています。
apps.apple.comまた、別のiPhone LiDARのアプリである、Scaniverseや3dScannerAppの使い方については以下の記事で説明しています。
もし、他のアプリについても興味のある方は以下の記事をご覧ください。
2. 使い方
2.1. New scanを選択する
赤枠で囲んだ、New scanを選択して、スキャンをはじめることができます。

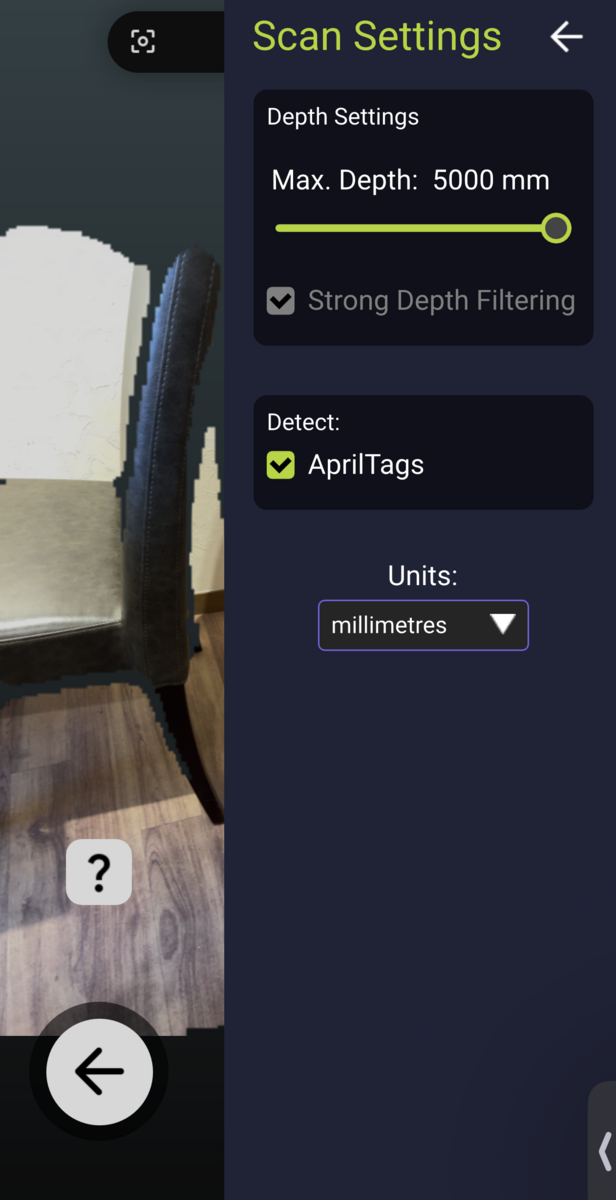
2.2. 設定の確認
以下の図の、歯車のマークを選択してください。

Max. Depthにて、最大どの範囲までをスキャンするかを決めることができます。iPhone LiDARでは5mほど離れた対象までをスキャンすることができます。
また、Detect: AprilTagsを有効にすることで、AprilTagを自動的に検出することができます。
2.3. スキャンの開始
真ん中下の立方体のアイコンをクリックすることで、スキャンを開始することができます。赤はスキャンされていない箇所を示しています。また、スキャンが進むごとに、Mappint: activeの値が増えていきます。

2.4. AprilTagの自動検出
Dot3Dの機能で、AprilTagの自動検出があります。あらかじめ、AprilTagの位置情報を取得しておくことで、後処理として、点群に正確な座標を与えることができます。AprilTagの位置情報に関しては、CSV形式であらかじめ用意しておきます。2.6にて説明します。

また、AprilTagはARの分野でも多く利用されます。以下の記事で、AprilTagを利用した簡単なデモについて仕組みを解説しています。
2.5. 結果の確認
スキャンを終了するときは、再び真ん中下のアイコンをタップします。これにより、以下のような3次元点群を生成することができます。

例えば、点に注釈をつける機能は以下のように利用することができます。
選択した点を長押しすると、拡大した図が表示されるので、そのマーカーの中心を選択したいときなどに便利です。長さを計測するときなども同様に点の位置を選択することができます。

2.6. ターゲットのインポート
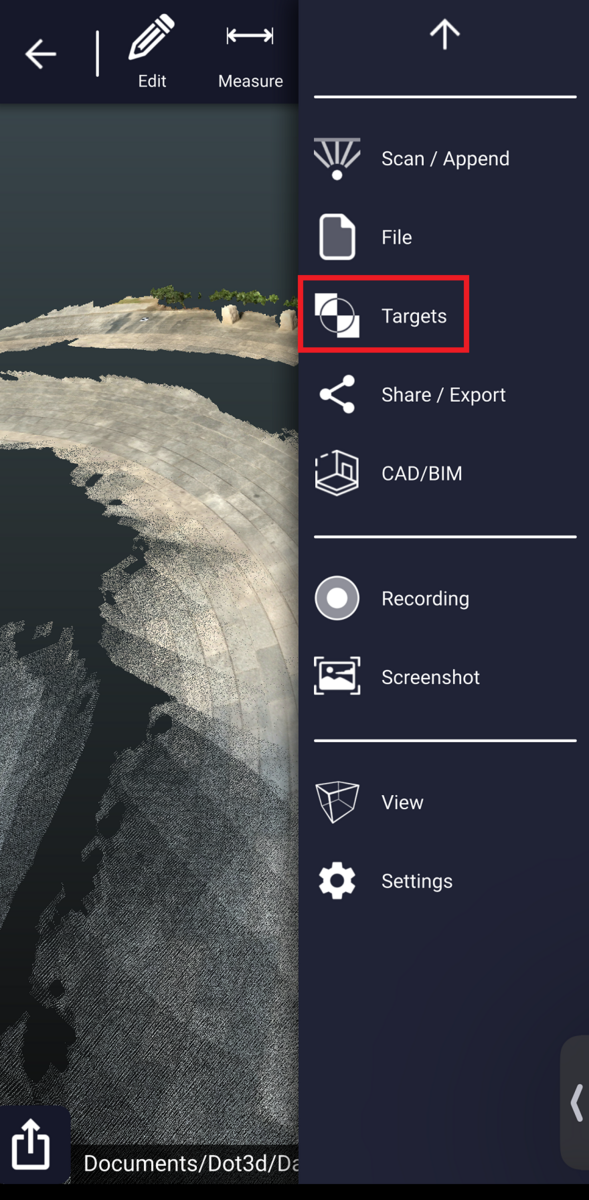
2.4にてAprilTagが自動的に検出されると述べました。次は、それぞれのAprilTagの座標の情報をインポートします。これにより、点群の位置を補正することができます。
右側のタブからメニューを開き、Targetsを選択します。
Load Control Fileを選択します。
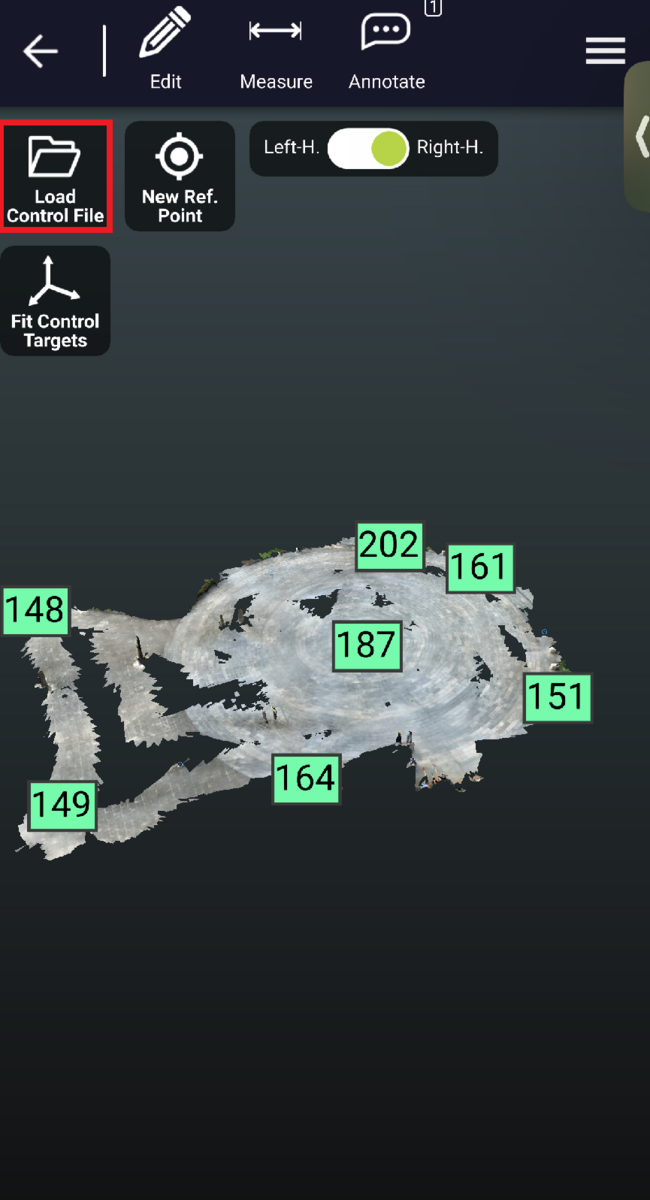
Open Control Fileを選択します。
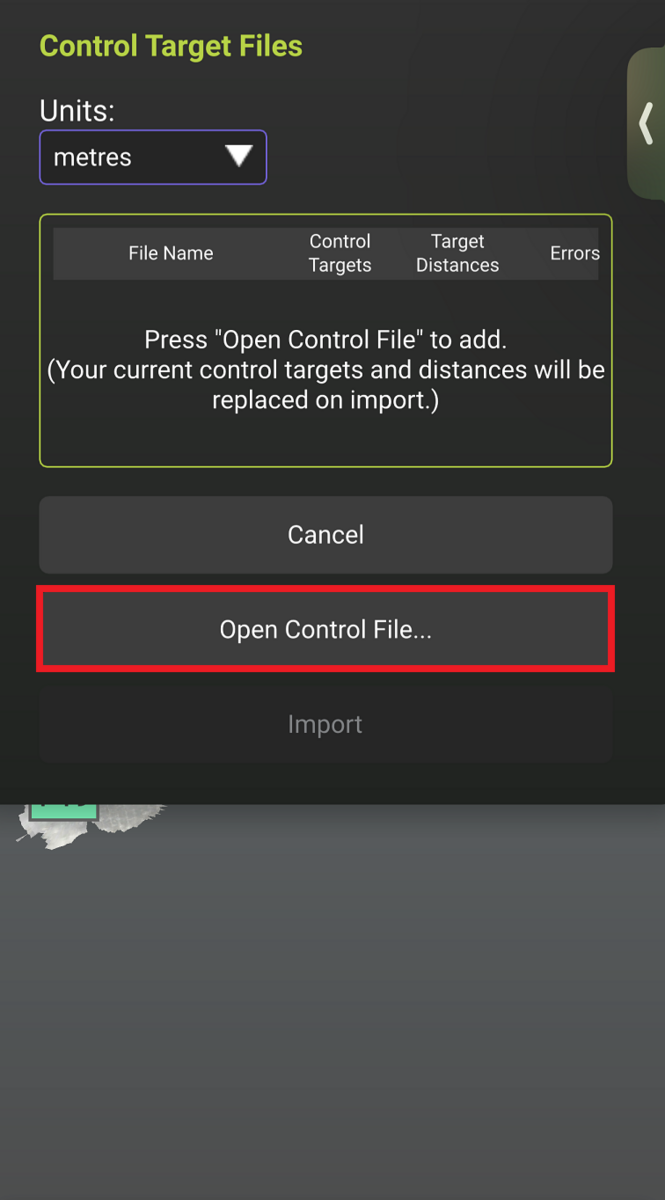
ここで、あらかじめ用意しておいたCSVファイルをインポートします。一番左の列にAprilTagのIDを入力し、その横にそれぞれXYZ座標を記載します。
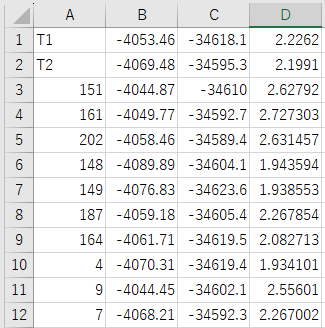
以下に、今回使用したCSVファイルを示します。なお、ファイル名に日本語が含まれているとエラーになる場合があります。半角英数字にてファイルを保存することが望ましいです。
ここでは、インポートしたCSVファイルの座標値を真値として、AprilTagの中心の位置との差が最小になるように、3次元上での回転や平行移動のパラメータを決定し、3次元のヘルマート変換のようなことを行っていると思われます。
また、Dot3Dに座標の情報をインポートする際、XYの入れ替え操作が発生する場合があります。 例えば、座標を測量座標系で用意していて、Xを北南方向、Yを東西方向に対応させている場合、 XとYの列を入れ替えて、数学座標系の形にしておく必要があります。 入れ替えに関しては、単にXとYの列を交換するだけで構いません。
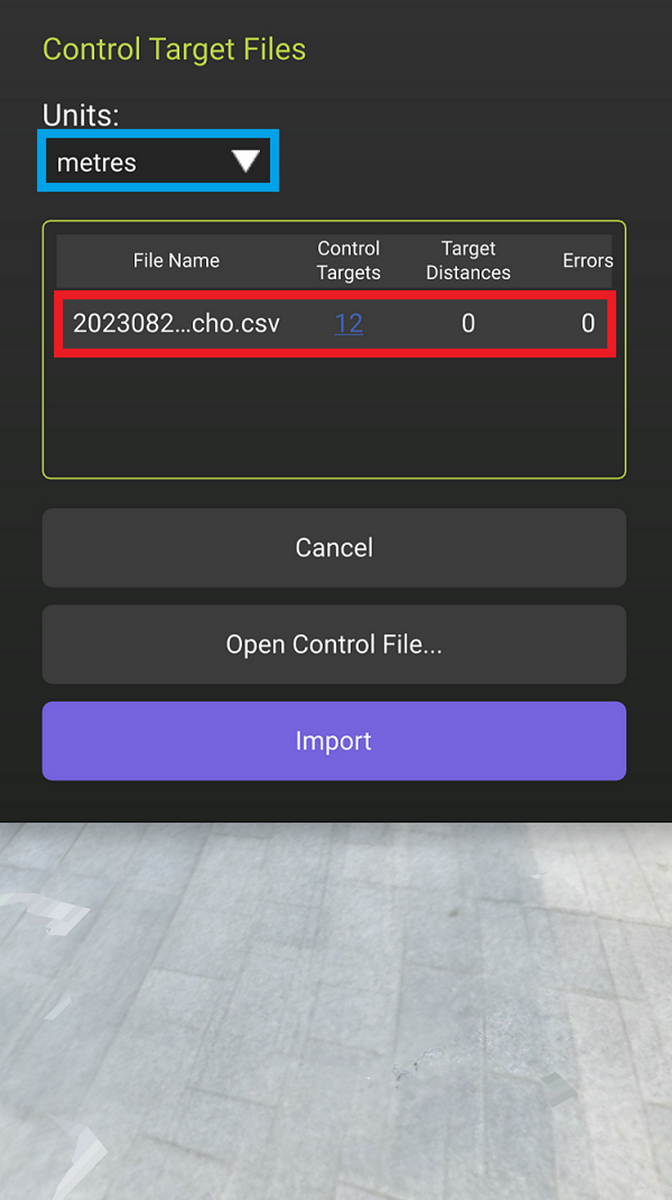
CSVファイルの読み込みが完了すると、以下のような画面になります。赤枠のように、インポートしたファイル名が表示されます。また青枠のように単位が正しく(今回はメートル)なっていることを確認します。
インポートを行ったのち、fit control をタップしてください。
fit controlが完了すると、以下のようなポップアップが表示されます。
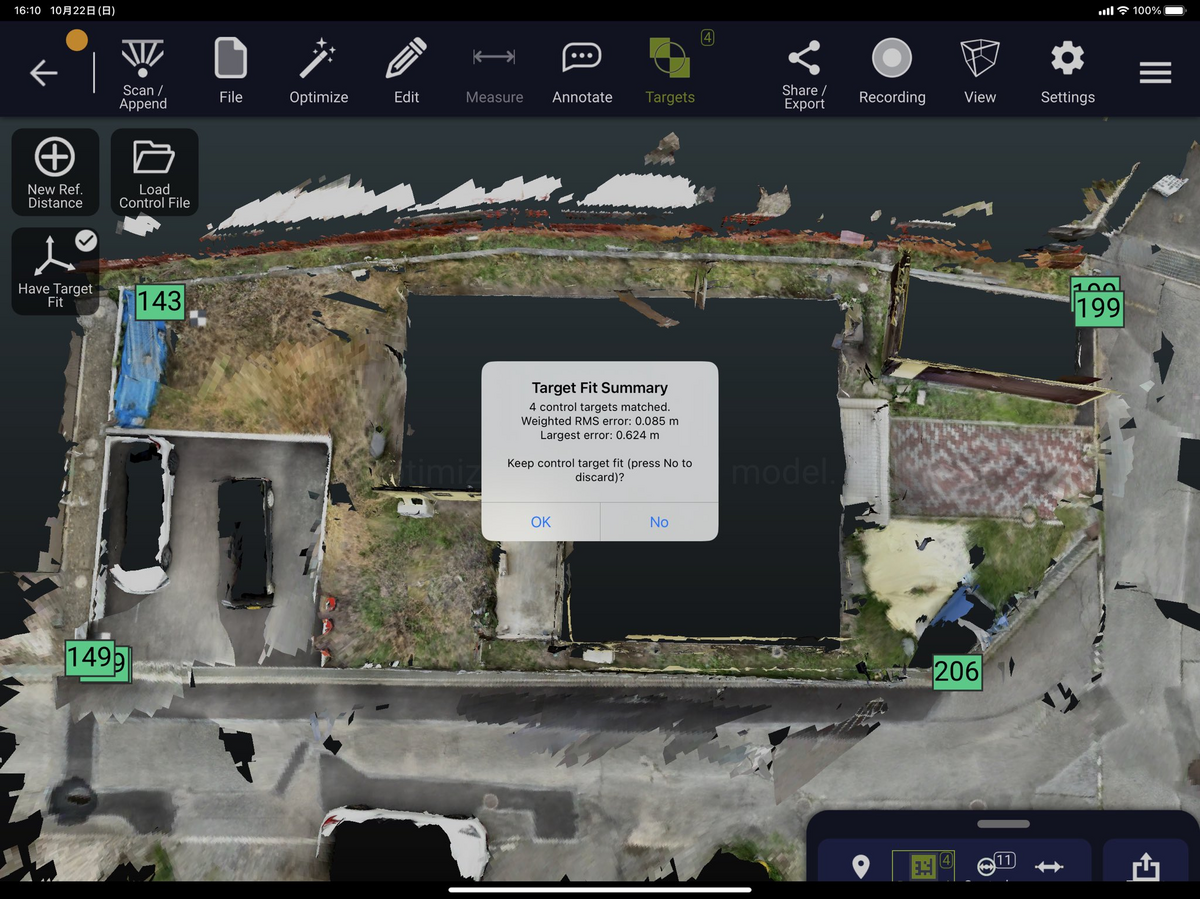
その後に、Optimizeを選択することで、点群の補正が完了します。
Optimizeの設定を選択すると以下のように表示されます。

Optimizeするために、少し時間がかかる場合があります。
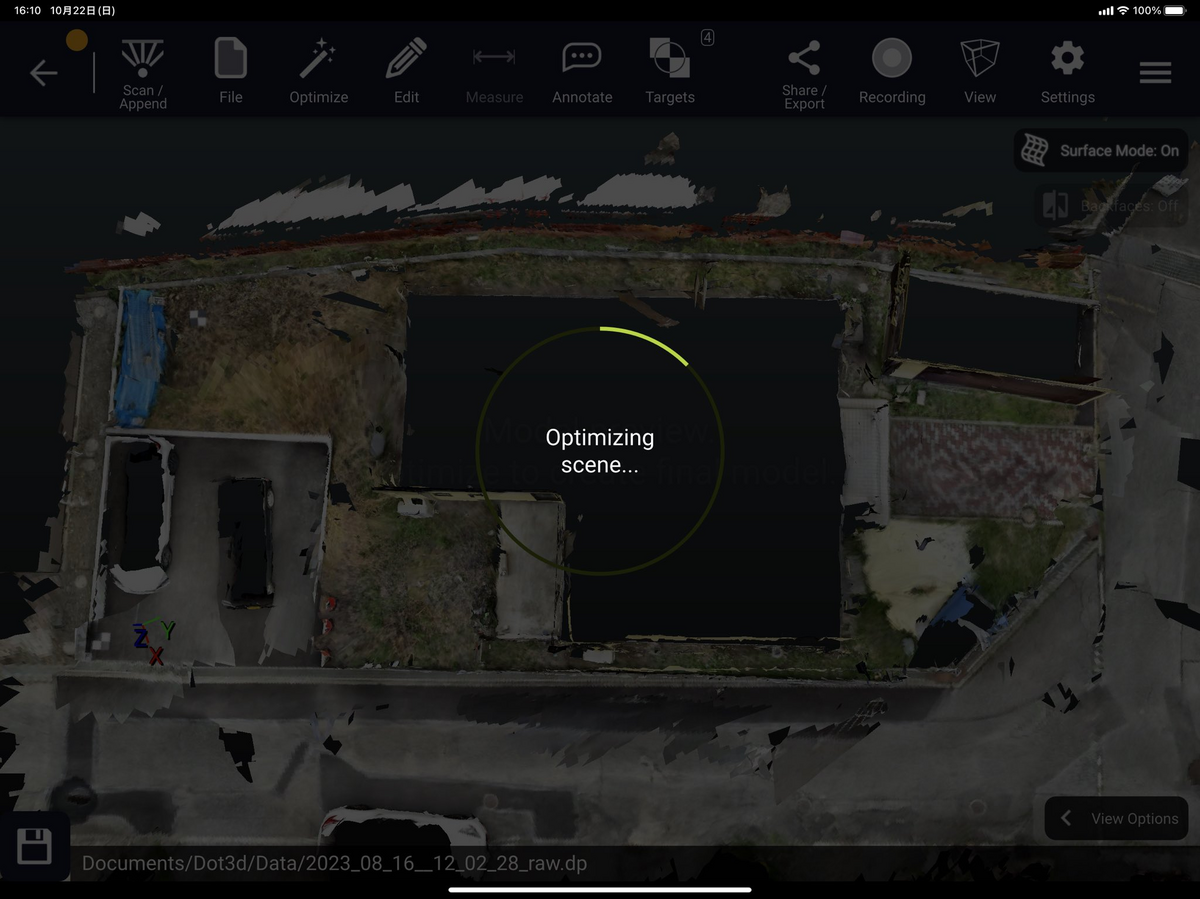
以下のように、AprilTagの中心にIDが打たれており、うまくインポート・補正ができたことがわかります。

2.7. 点群のエキスポート
ここで取得した点群ファイルをエキスポートし、他のソフトウェアで閲覧したいと思います。右側のメニューから、Exportを選択して下さい。
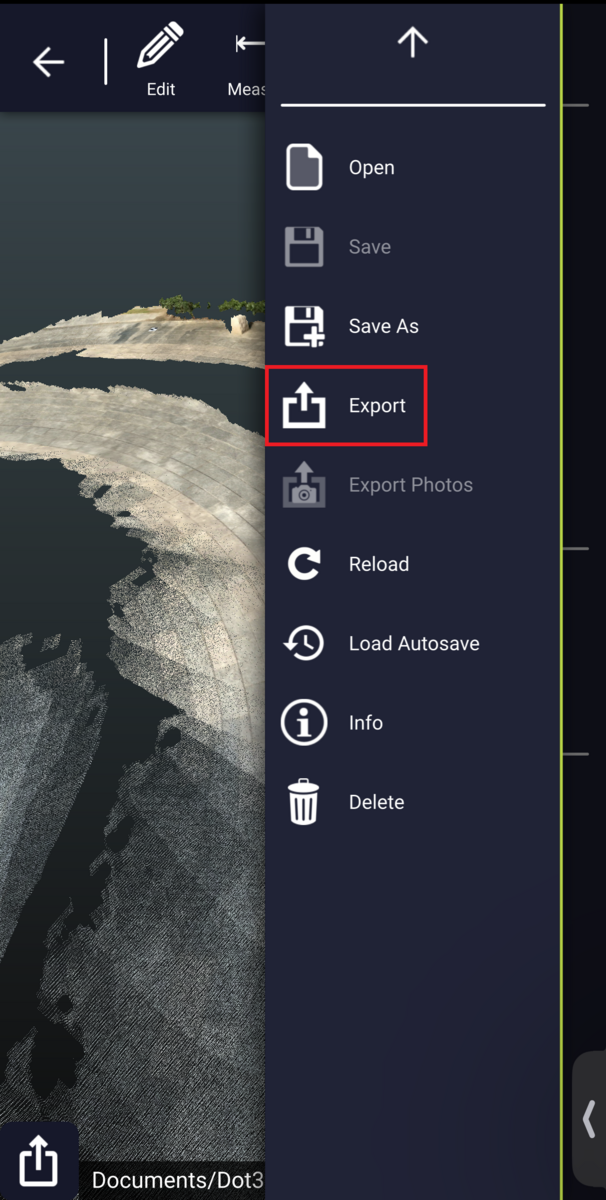
拡張子を選択します。LAS、LAZだけでなく、多くのフォーマットが用意されています。私はSLACKのダイレクトメッセージで自分に送信し、PCでダウンロードできるようにしました。
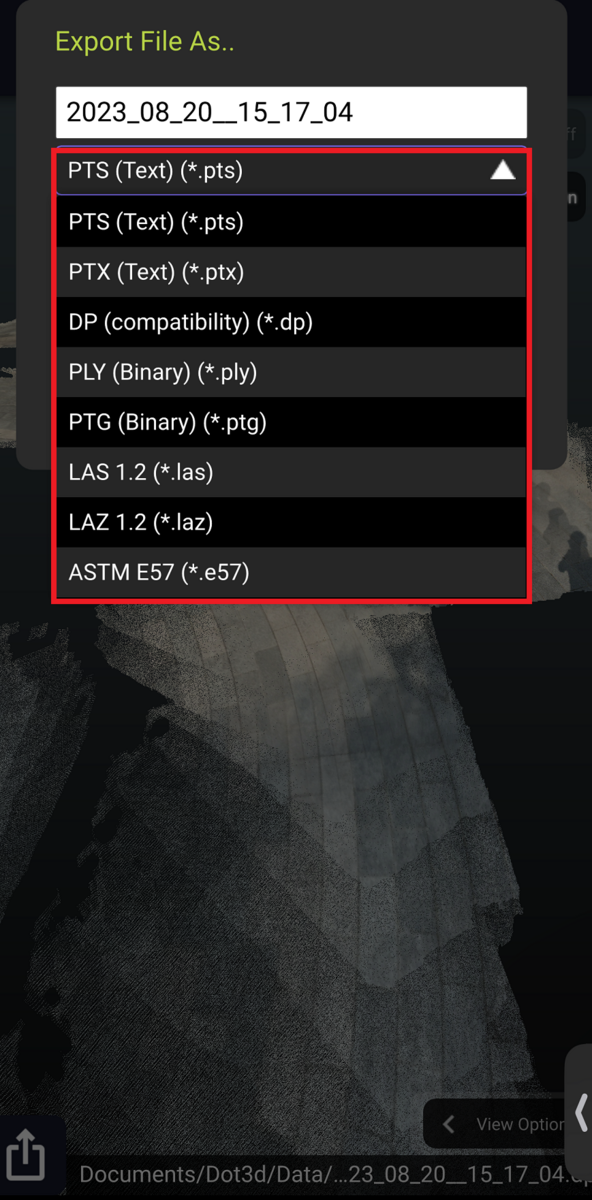
例えば、PTSフォーマットに関しては以下の記事で紹介しています。
最後にエキスポートするオプションを設定することができます。単位が私のアプリではmmになっていたので注意が必要です。例えば他のモデルや点群と重ね合わせたいときは、mで出力するほうが良いかもしれません。

また右のOptionsでは、間引きの割合を決めることができます。そのままエキスポートする場合は点群のファイルサイズが膨大で、うまくエキスポートが進まない場合もあるかもしれません。その場合は、ここの%の値を小さくするとファイルサイズが小さくなります。しかし必要とされる点群密度や精度が担保されるかは別途確認が必要です。ここでは、ランダムサンプリングを行っていると思われます。
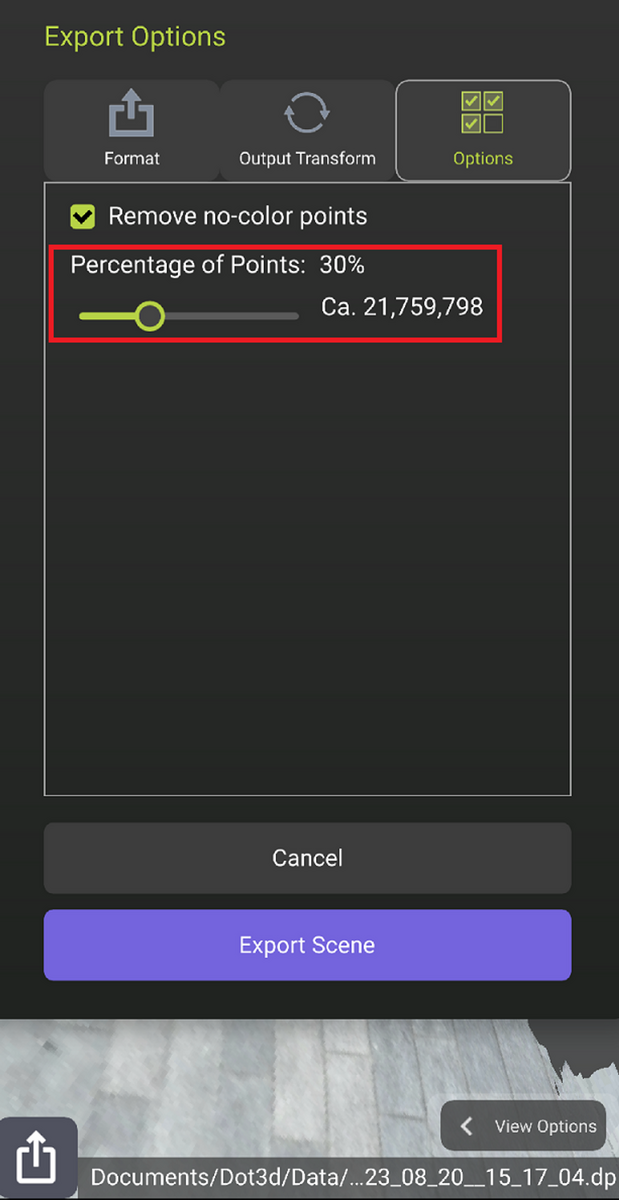
3. ScanXへの読み込み
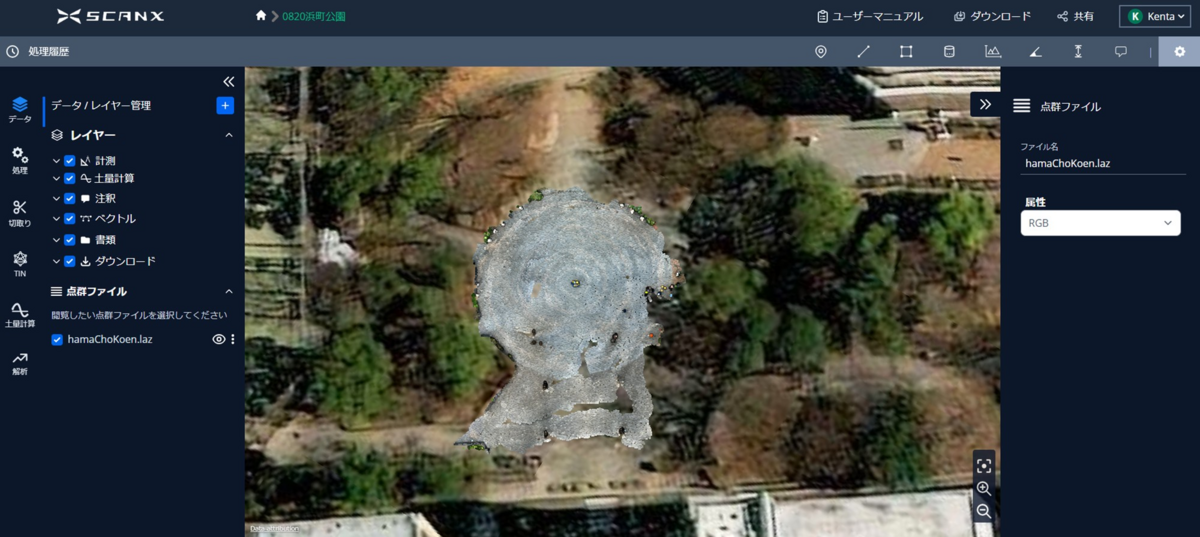
次に、Dot3Dで得た点群を別の点群処理ソフトウェアにインポートしてみたいと思います。ここでは、ScanXというオンライン型のソフトウェアを使いたいと思います。 ここでは、LAZ形式で保存した点群ファイルをScanXにアップロードしてみます。
3.1. RGB表示
ベースマップ上での位置:
地図上でうまく合ってるように見えます。
近づいた場合:
公園で撮った時は明るくてあまりスマホの画面が見えなかったのですが、PC上で見るとよりキレイに見えると感じました。

3.2. 地表面抽出の結果
地表面が自動的に抽出され、茶色で示されています。

3.3. 座標点インポートの結果
さきほどのCSVファイルを読みこみ、可視化してみました。AprilTagで検出された位置で補正しており、うまく座標点とAprilTagの位置が一致していることがわかります。

4. QGISへの読み込み
簡単に、GISソフトであるQGISにも読み込んでみたいと思います。ドラッグアンドドロップでLASファイルやLAZファイルをインポートできます。
2023年8月現在では、AprilTagを検出したとしてもDot3D上で、EPSGコードを入力する画面がないため、LAS/LAZファイルのメタ情報にEPSGコードの情報は入っていませんでした。
そのため、QGIS上で、EPSGコードを入力する必要があります。今回はEPSGコード6677を指定しました。
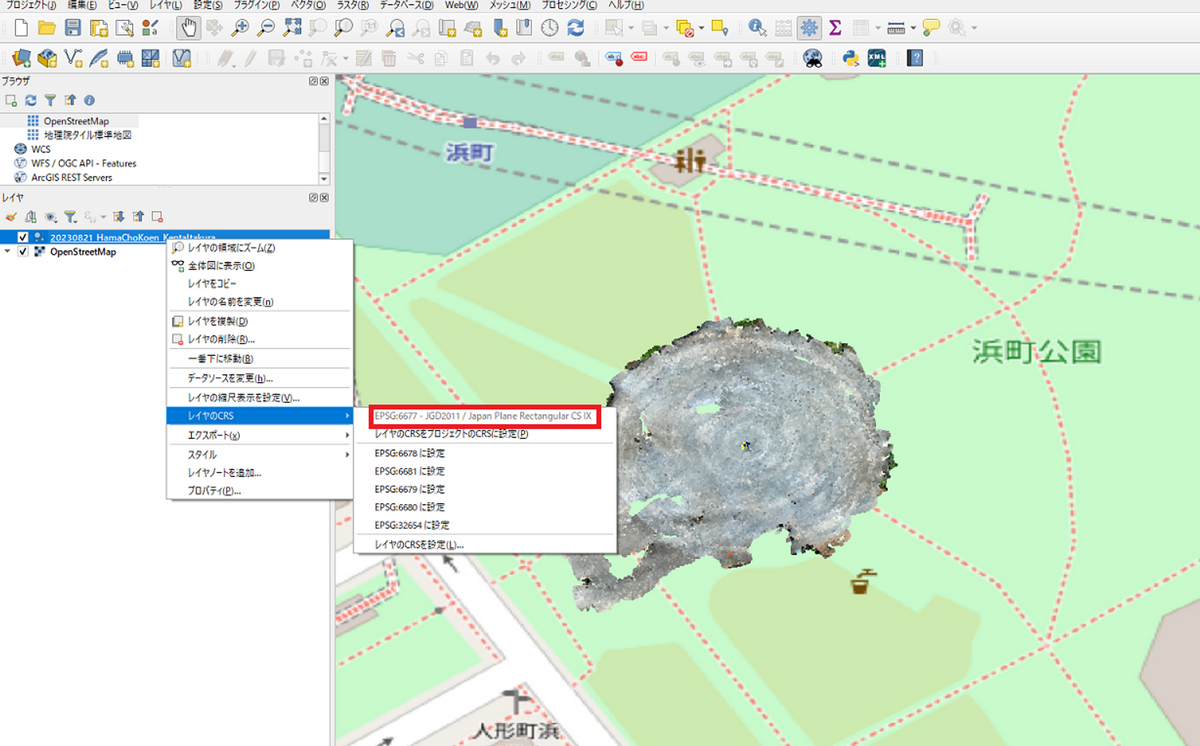
メタ情報を確認してみます。
CRS: 手動で入力しました。
LASのバージョン: 1.3でした。Dot3D上では1.2となっていましたが、実際は1.3のようです。
縮尺: 0.01mmでした。うまくDot3Dで測量できていればLASでエキスポートしたときも精度は保たれていそうです。
色情報: 16bitで保存されていました。

5. まとめ
この記事では、LiDARを搭載したiPhoneにて、Dot3Dを利用し、対象をスキャンする方法について述べました。わかいやすい操作画面で、非常に使いやすかったです。また、AprilTagの自動検出が正確で、LiDAR点群の位置補正を簡単に行うことができました。
ファイルサイズの大きいJSONファイルの読み込み
はじめに
非常に多くの行数のあるJSONファイルをPythonで読み込む方法について備忘録として残します。
以下の、izumi-lab/llm-japanese-dataset の一部を取り出して保存してみたいと思います。
拡張子を手動で.jsonlから.jsonに変更しました。
あらかじめ、こちらのJSONファイルををダウンロードしているとします。
また、本記事で利用したコードは以下のページにアップロードしています。
Pythonコード
モジュールのインポート
import json import codecs
ジェネレータ関数を作成する
def read_json_file_in_batches(file_path, batch_size): with open(file_path, 'r', encoding='utf-8') as file: batch = [] for line in file: batch.append(json.loads(line)) if len(batch) == batch_size: yield batch batch = [] # すべてを読み取ったあと、batchにまだ中身があればyieldする if batch: yield batch
保存するファイル名を指定する
output_file_path = 'output.json'
練習のため、次の日本語を英語に翻訳してください という文章を含む行が現れるまで読み込みます。また、それまでの行の情報をlistに格納していきます。
# 指定した文字列が見つかったかどうかを示すflagを用意する flag = False in_file_path = 'data-cc-by-sa.json' batch_size = 10 search_string = "次の日本語を英語に翻訳してください" output = [] for json_batch in read_json_file_in_batches(in_file_path, batch_size): # json_batchは最大でbatch_size行のJSONオブジェクトを含むリストである # 1行ずつ読み込んでいく for json_object in json_batch: # 指定した文字列が含まれるか判定する if any(search_string in value for value in json_object.values())==True: print('指定した文字列が含まれます') print(json_object) flag = True # 指定した文字列が見つかるまでリストに文章を追加していく output.append(json_object) # 指定した文列が含まれていた場合ループから抜け出す if flag: print('BREAK') break # 指定した文列が含まれていた場合ループから抜け出す if flag: break
ファイルの書き込み
fw = codecs.open(output_file_path , 'w', 'utf-8') json.dump(output, fw, ensure_ascii=False, indent=0) # 書き込みオブジェクトを閉じる fw.close()
以下のように 次の日本語を英語に翻訳してください が含まれる文章までのデータを書き込むことができました。

