この記事はMATLAB/Simulink Advent Calendar 2023の16日目の記事として書かれています。

1. はじめに

3次元点群データは、XYZの点の集まりで表現されますが、「地球上での位置」を示すこともできます。
以下の図は、無料のGISソフトウェアであるQGISを利用して、地図上に3次元点群データを表示しています。

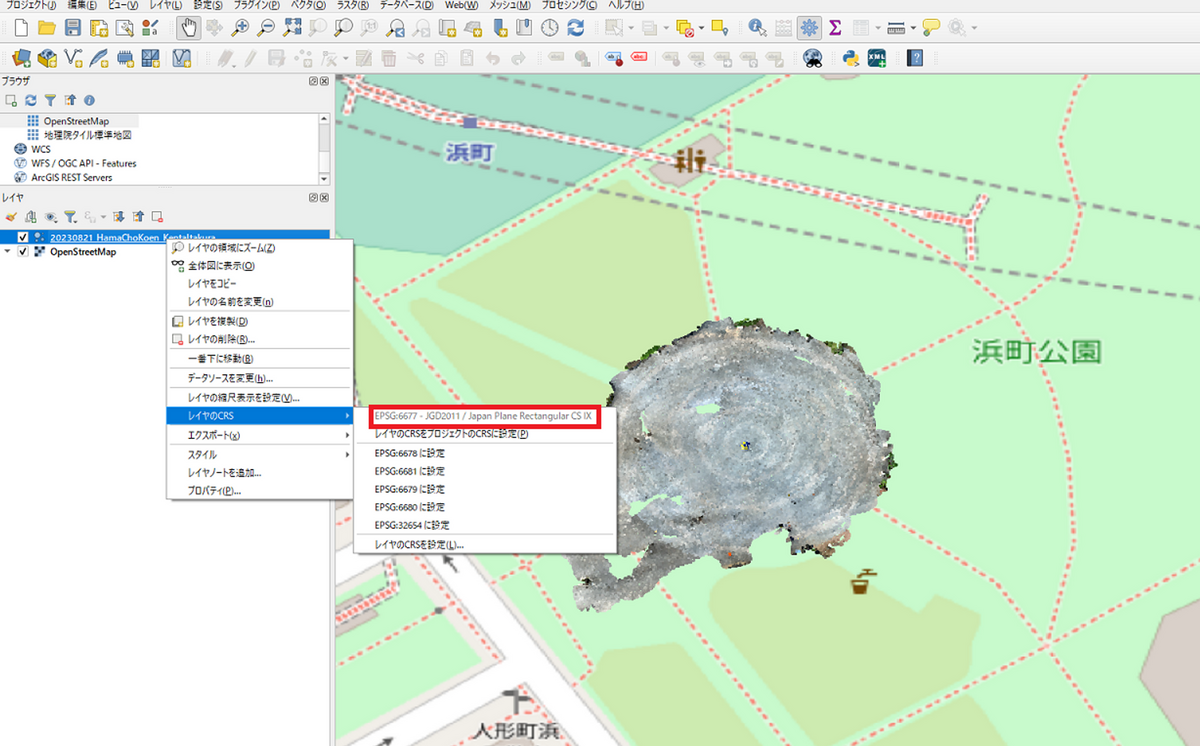
この際に、座標参照系（CRS）やEPSGコードというものを設定する必要があります。
この記事では、3次元点群データを地図上で見るために必要な座標参照系（CRS）やEPSGコードについてまとめます。

3次元点群データはiPhoneに搭載されたLiDARを利用して取得することもできます。
3次元点群データをiPhoneからエキスポートする様子については以下の記事をご覧ください。

kentapt.hatenablog.com

2. EPSGコードについて

2.1. 地球上での点の位置を表す

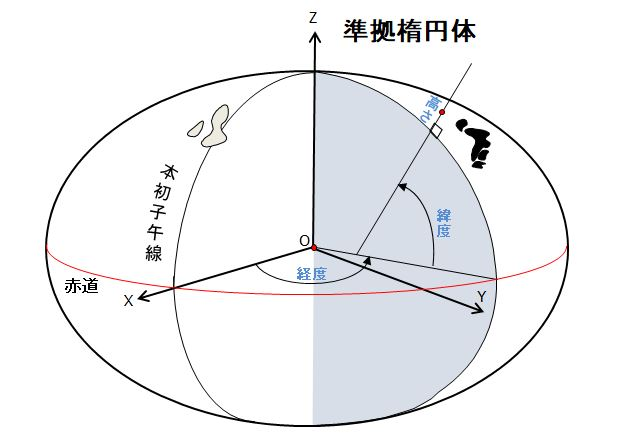
　取得した点群を地図上で表示させるためには、その点群が地球上のどこに位置するかを表す必要があります。以下の図のように、地球上の位置は、経度や緯度、高さの情報などを用いて表すことができます。以下の図では、きれいな楕円体の中での、位置を求めていますが、実際は、場所によって高低差があったり、複雑な地形をしていたり、単純に楕円体で地球を表すことは簡単ではありません。

　また、シンプルかつ、地球の形状をうまく表現する楕円体を用意したのち、3次元的な地球（儀）で位置を表現するよりも、一部の領域であれば、2次元の平面に投影してしまっても実用上問題はありません。このように地球上での点群の位置を表すためにはいくつか方法があり、どのような方法をもとに表しているかを示す番号（のちに説明するEPSGコードに相当）があると便利そうです。地球上での位置を表す方法について、測地系と座標系に分けて説明します。

画像出展：国土地理院　日本の測地系より

2.2. 測地系

測地系とは

その経度・緯度の座標で表す時の座標の基準(点)
地球を楕円体とみなすときの形状

などを定義するための基準です。これにより、地図を作成する時や、測量時において、共通して地球上の位置を表現することができます。これにより、点群を正しく地図上で閲覧することができます。

　測地系の中でも、世界測地系や局所測地系などが存在します。世界測地系は、国際的に定められた測地系です。一方、局所測地系は、その地域の近傍に対して適用できる測地系です。

　局所測地系の例として、改正測量法の施行前は、明治時代に採用したベッセル楕円体という楕円体を地球を表すために用いていました。そして、これをもとにして、東京天文台の経度・緯度が、天文観測にて求められ、日本の原点の位置として決められました。

　その後、VLBIや人工衛星などの技術の進歩により、より正確な地球の形状や大きさが求められるようになり、地球全体によく適合した測地基準系として、世界測地系が構築されました。　

2.3. 座標系

　地球上の点の座標を定める上で、測地系の他に、座標系について考える必要があります。座標参照系は大きく分けて、「地理座標系」「投影座標系」の２種類があります。この節では、この2種類の座標系について述べます。

2.3.1 地理座標系

地理座標系では、その点の位置を経度や緯度を用いて表します。

2.3.2 投影座標系

投影座標系では、一部の（限られた）範囲を2次元の平面へ投影する狭い範囲の一部を平面へ投影したときの座標を示します。ここでは、その投影した時の原点からのx方向およびy方向の値をもって、その点の位置を示すことができます。

投影の方法は複数存在し、以下の図のように

円筒図法
円錐図法
方位図法

といった投影方法が存在します。

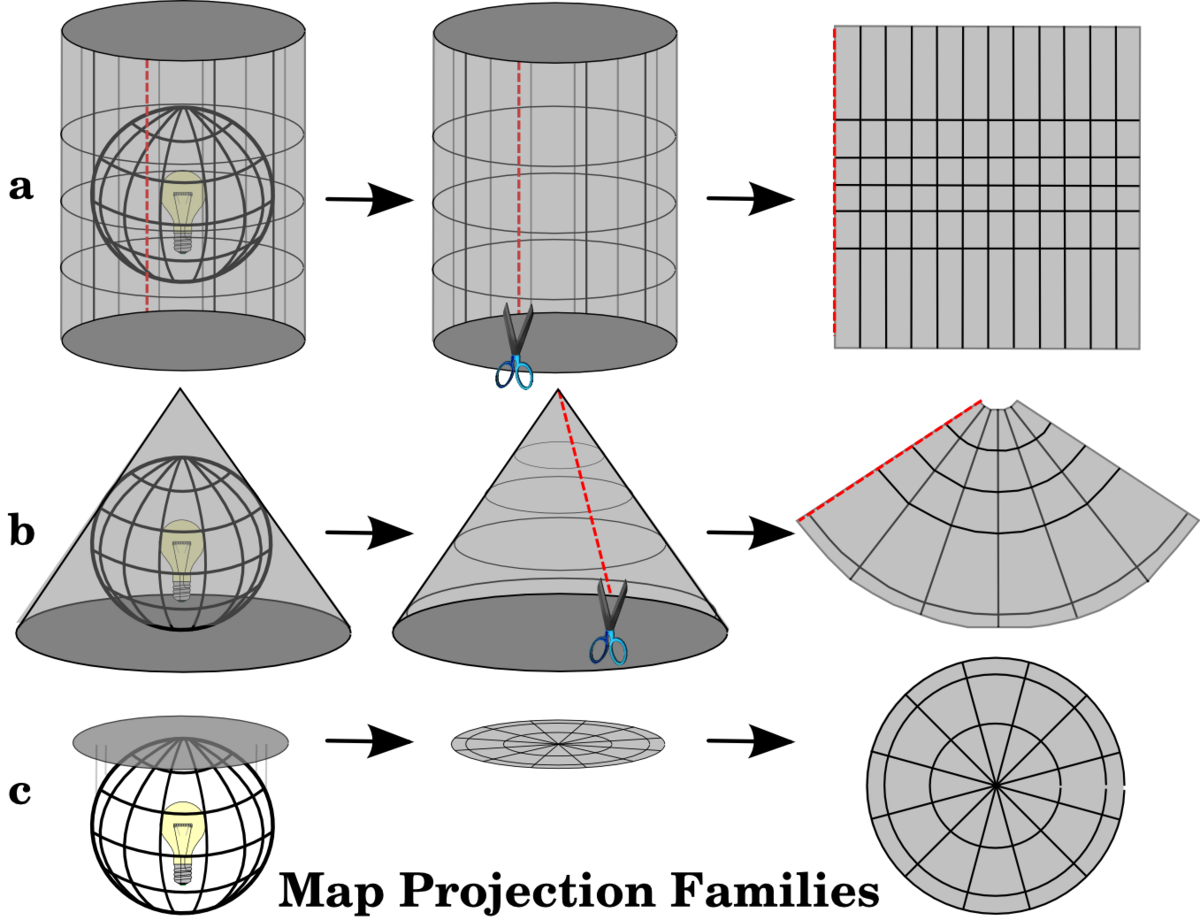
図出展: QGI documentation Coordinate Reference Systems ********(https://docs.qgis.org/2.8/en/docs/gentle_gis_introduction/coordinate_reference_systems.html)

2.4. 空間参照系

2.2で述べた測地系や2.3で述べた座標系の組み合わせによって、空間参照系を定義することができます。

測地系では、

地球を楕円体とみなした時の形状の詳細
楕円体とみなした時の原点

などが決められ、

座標系では、

経度や緯度を用いて表す
投影座標を用いて表す
- どのような投影方法を用いるのか
- どの場所を投影するときの原点とするのか

といったことが決められるのでした。

このような掛け合わせを経て、地球上の点の位置を定めるためのパターンは非常に多く存在します。そこで、空間参照系を識別するためのコードがあると便利です。

本図は、地図のワークブック空間参照系（測地系/座標系/投影法）について (https://lonlat.info/spatialreferencesystem/) を参考に作成されました。

3. MATLABで点群の座標を経度・緯度に変換する

MATLABで点群の位置座標を変換してみます。データは、iPhone LiDARのアプリである、iPhone LiDARのアプリである、Scaniverseを利用して取得された点群を利用します。主に、Mapping Toolboxを利用します。

以下のように対象の点群をMATLAB上でくるくると回すことができます。Scaniverseで取得された取得された点群をLAS形式でエキスポートした場合、UTM座標系が利用されます。

この点群のXYZ座標を読み取り、経度・緯度に変換したいと思います。

利用した点群データは以下にアップロードされています。ぜひダウンロードして、以下のコードを実行してみてください。

github.com

流れは以下の通りです。

readPointCloud 関数を利用して点群の読み取り
projcrs 関数を利用して、UTM54Nの projcrs オブジェクトを作成する
projinv 関数を利用して、UTM54Nの座標を経度・緯度に変換する
geoscatter 関数を利用して、地図上にプロット

clear;clc;close all
% las/lazファイルを読み込むためのlasFileReader objectを作成する
lasReader = lasFileReader('treeTrunk.laz');
% las/lazファイルの、xyzおよび色情報を読み込み
ptCloud = readPointCloud(lasReader);
% projcrsオブジェクトを作成する
utm54N = projcrs(32654);
% projinv 関数を利用して、UTM54Nの座標を経度・緯度に変換
[lat,lon] = projinv(utm54N,ptCloud.Location(:,1),ptCloud.Location(:,2));
% スムーズに可視化するため、点をサンプリング
idx = randperm(ptCloud.Count,100000);
% 色の取り出し
ptCol = ptCloud.Color(idx,:);
% 地図上にプロット
geoscatter(lat(idx),lon(idx),1,single(ptCol)./2^16)