サポートベクターマシン(SVM)の分離平面の可視化 (Python, MATLAB)
この記事では、サポートベクトルマシン(SVM)を用いて、分類を行ったときの、分離のための超平面を可視化することを行います。PythonとMATLABにて書いてみたいと思います。ここでは、3つの変数を説明変数として用いて、3次元プロットによる可視化を行います。
可視化におけるポイントは、
1. XYZの範囲内でその値を小刻みに変更しながらグリッドを作成する
2. そのデータに対してSVMによる分類を行う
3. そのときの結果の中で、分類平面に近いデータを取り出す
4. そのデータを訓練データと重ね合わせて表示する
ということです。
コードは以下のページにアップロードしています。
モジュールのインポート
この例では、jupyter notebookを用いています。点を3D上でプロットして、くるくると回すために、%matplotlib notebookと指定します。
from sklearn.svm import SVC import numpy as np import matplotlib.pyplot as plt from sklearn import svm, datasets from mpl_toolkits.mplot3d import Axes3D from scipy.interpolate import griddata %matplotlib notebook
irisデータセットの読み込み
ここでは、irisデータセットを用います
iris = datasets.load_iris() X = iris.data[:, :3] # 3つの変数のみを用いる Y = iris.target # 用いるデータの作成 X = X[np.logical_or(Y==0,Y==1)] Y = Y[np.logical_or(Y==0,Y==1)]
SVMの学習
ここでは、ガウシアンカーネルを用いて学習を行います。線形カーネルで行う場合は、"linear"と指定します。
# 分類器の準備 model = svm.SVC(kernel='rbf',probability=True) # 学習 clf = model.fit(X, Y)
分離平面を可視化するためのテストデータを作成する
各変数の最大値と最小値を求め、その範囲でテストデータを作成します。mesh_sizeという変数で、その間隔を制御します。小さい値に設定すると、より厳密な分離平面を得ることができますが、一方で、計算時間が長くなります。
# データを作成する間隔 mesh_size = 0.2 # 変数をそれぞれ、x1, x2, x3とする x1 = X[:,0] x2 = X[:,1] x3 = X[:,2] # 作成する範囲を大きくしたい場合marginを0より大きい値にする margin = 0 # xyzの最小、最大値を求める x_min, x_max = x1.min() - margin, x1.max() + margin y_min, y_max = x2.min() - margin, x2.max() + margin z_min, z_max = x3.min() - margin, x3.max() + margin # mesh_sizeに応じて点を作成する xrange = np.arange(x_min, x_max, mesh_size) yrange = np.arange(y_min, y_max, mesh_size) zrange = np.arange(z_min, z_max, mesh_size) x,y,z = np.meshgrid(xrange,yrange,zrange) # flatten x = x.reshape(-1) y = y.reshape(-1) z = z.reshape(-1)
分離平面を可視化するためのテストデータと訓練データを重ね合わせる
前のセクションで作成したテストデータが、訓練データと重なっているかを確認する
# 可視化 fig = plt.figure() ax = fig.add_subplot(projection='3d') # テストデータのプロット ax.scatter(x, y, z) # 訓練データのプロット ax.plot3D(X[Y==0,0], X[Y==0,1], X[Y==0,2],'ob') ax.plot3D(X[Y==1,0], X[Y==1,1], X[Y==1,2],'sr') plt.show()

テストデータの予測
xyz = np.vstack([x,y,z]) xyz = xyz.T y_pred = clf.predict_proba(xyz)
クラスAとBの確率が等しいテストデータを抽出
diff = y_pred[:,0]-y_pred[:,1] idx = np.where(np.abs(diff)<0.1) xyz = xyz[idx,:] out = np.squeeze(xyz)
分離平面の可視化
最後に、前のセクションで取り出した点ともとの訓練データを重ねて表示させます。これにより、うまく分離平面が可視化できていることがわかります。
# クラスAとBの確率がほぼ等しい点のx,y,z情報を抽出する x_selected = out[:,0] y_selected = out[:,1] z_selected = out[:,2] # surfaceプロットをするための準備 x_new, y_new = np.meshgrid(np.unique(x_selected), np.unique(y_selected)) z_new = griddata((x_selected, y_selected), z_selected, (x_new, y_new)) # 可視化 fig = plt.figure() ax = fig.add_subplot(projection='3d') ax.plot3D(X[Y==0,0], X[Y==0,1], X[Y==0,2],'ob') ax.plot3D(X[Y==1,0], X[Y==1,1], X[Y==1,2],'sr') # surfaceの可視化 ax.plot_surface(x_new, y_new, z_new,cmap='plasma') ax.set_xlabel(r"$x_1$", fontsize=12) ax.set_ylabel(r"$x_2$", fontsize=12) ax.set_zlabel(r"$x_3$", fontsize=12) ax.set_title("Visualizing hyper-plane", fontsize=12) plt.show()
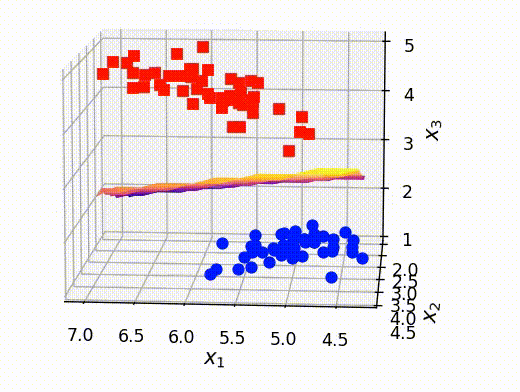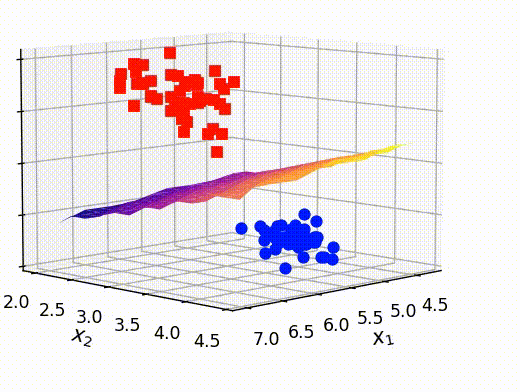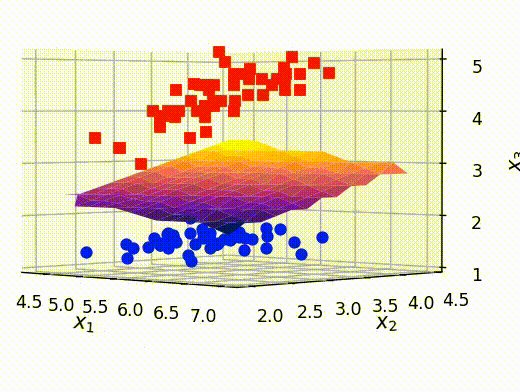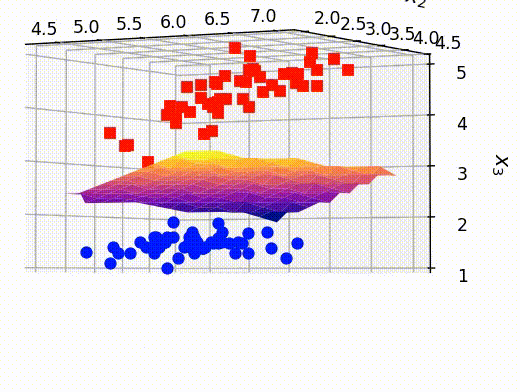
参考文献
以下の記事などが参考になりました。著書の皆様、ありがとうございました。