iPadで数式を書いて、MATLAB livescriptでブログ記事を書いてみよう
この記事は、MATLABアドベントカレンダー（その2）の19日目の記事として書かれています。
はじめに
私が数式を含むブログ記事を投稿するときの手順を紹介したいと思います。あくまで私が気に入っている方法であり、他にもよい方法があると思います。参考になれば幸いです。
例えば、以下のような数式が多い記事をブログ投稿したい場合を考えます。
そのような場合は、ここで紹介する方法が効果的でした。
大まかな手順として、以下の流れを想定しています。
1 内容をまとめ、ブログに掲載する数式を用意する
2 記事を執筆する
3 ブログ投稿がしやすい形で記事や画像をエキスポートする（マークダウン形式）
4 記事を投稿する
ここでは以下のものが必要です。
手順
手順1 内容をまとめ、ブログに掲載する数式を用意する
はじめに、ブログに書くような数式やその流れを考える必要があります。ここではその作業が完了していることを想定します。私は、以下のアプリを利用しています。もし、iPadをお持ちの方はぜひダウンロードしてみてください。
使い方は簡単です。以下の赤枠で示されているように、数式を入れるモードがあるので、そこで、以下のようにどんどん数式を書いていきます。
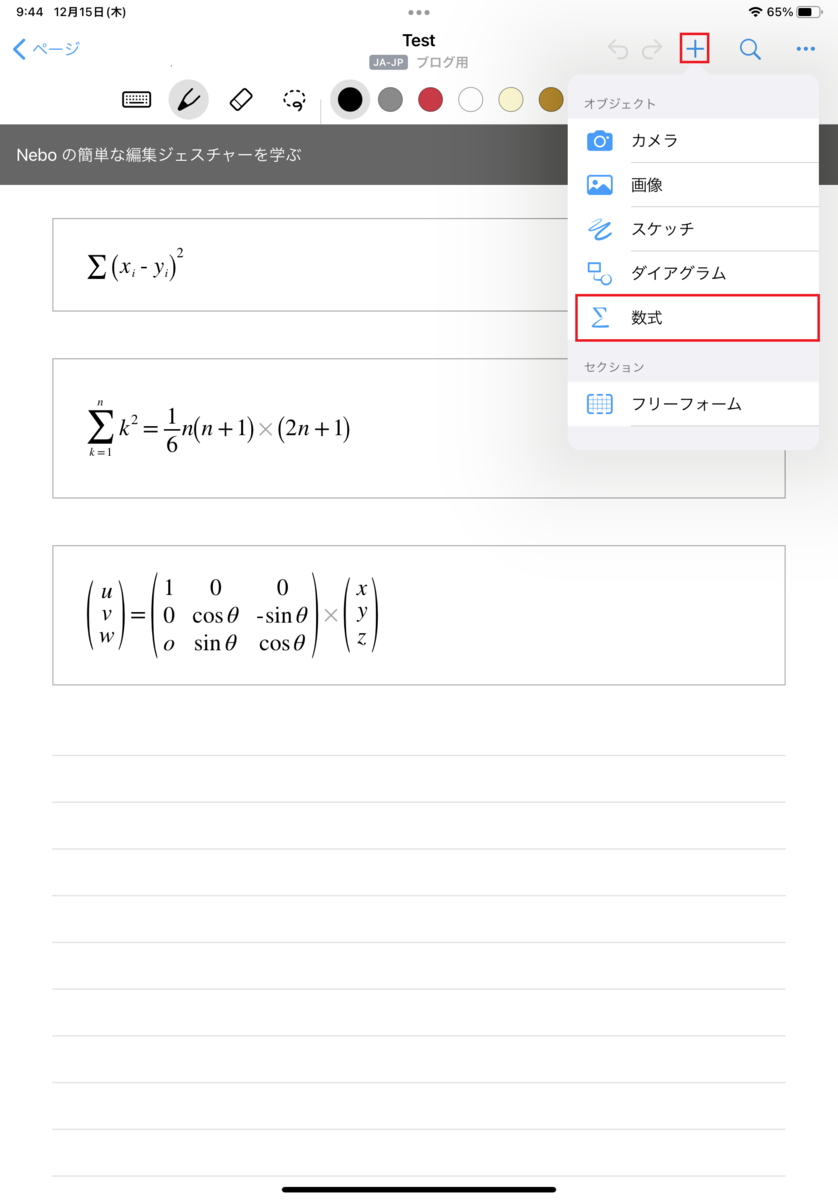
ある程度数式がかけたら、右上の、「三つの点・・・」のボタンを選択して、数式に変換してください。
すると、以下の動画のように、高精度で数式を認識して、自動変換してくれます。これよりも複雑なものでも問題ありませんでした。
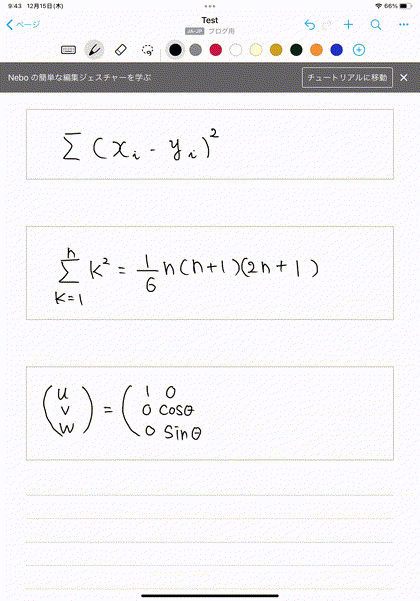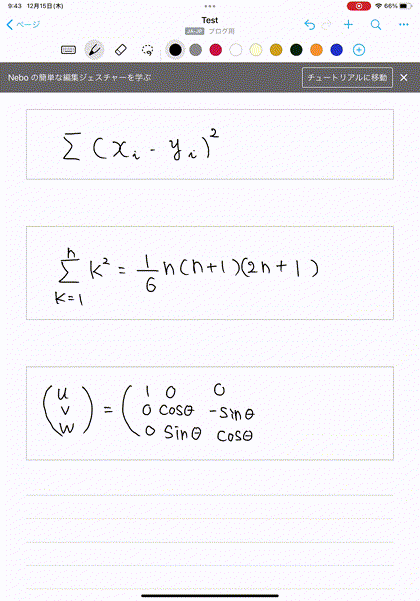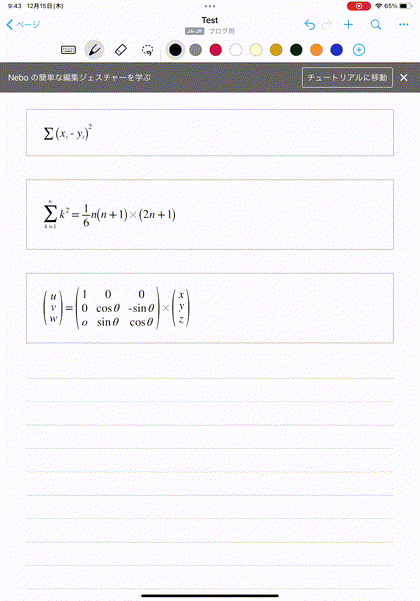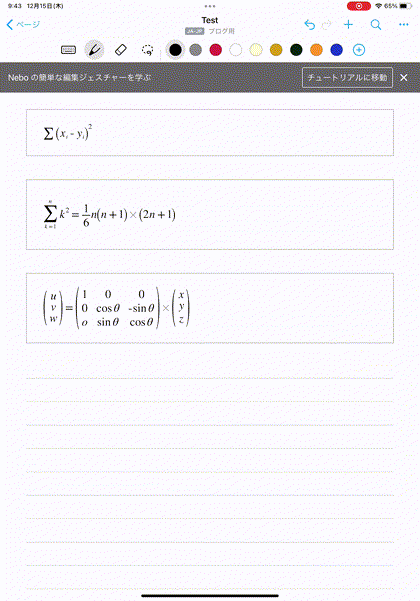
このような数式の書き込みを重ねて、記事に必要な数式が書けた場合を考えます。
次のステップとしては、このiPad上の数式をブログ投稿できる形でエキスポートします。 以下のボタンをタッチしてください。
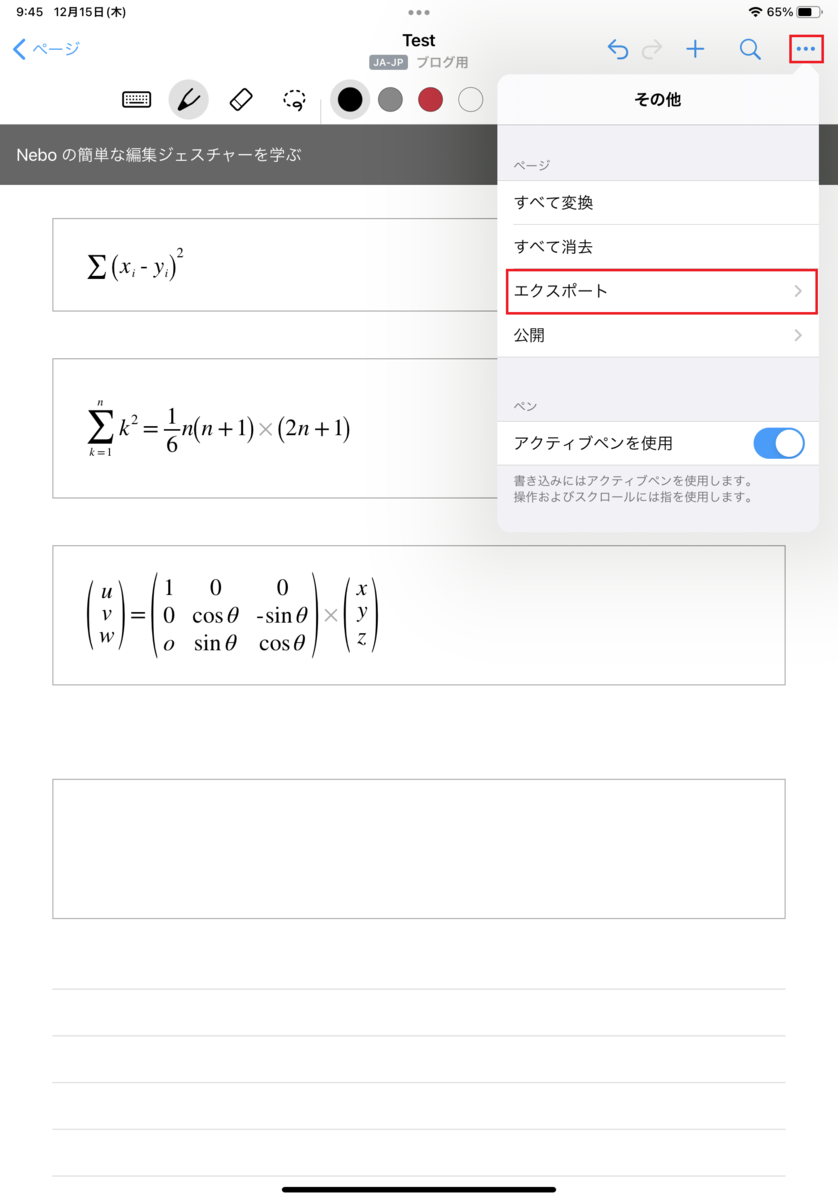
出力形式はWordを選択します。
このように、簡単なタッチ操作で、iPadで書いた数式をWordにエキスポートすることができます。（もしかしたらこのあたりで少し課金が必要かもしれません）
この作業の後、Google Driveなどを経由して、Wordファイルとしてエキスポートが可能になります。
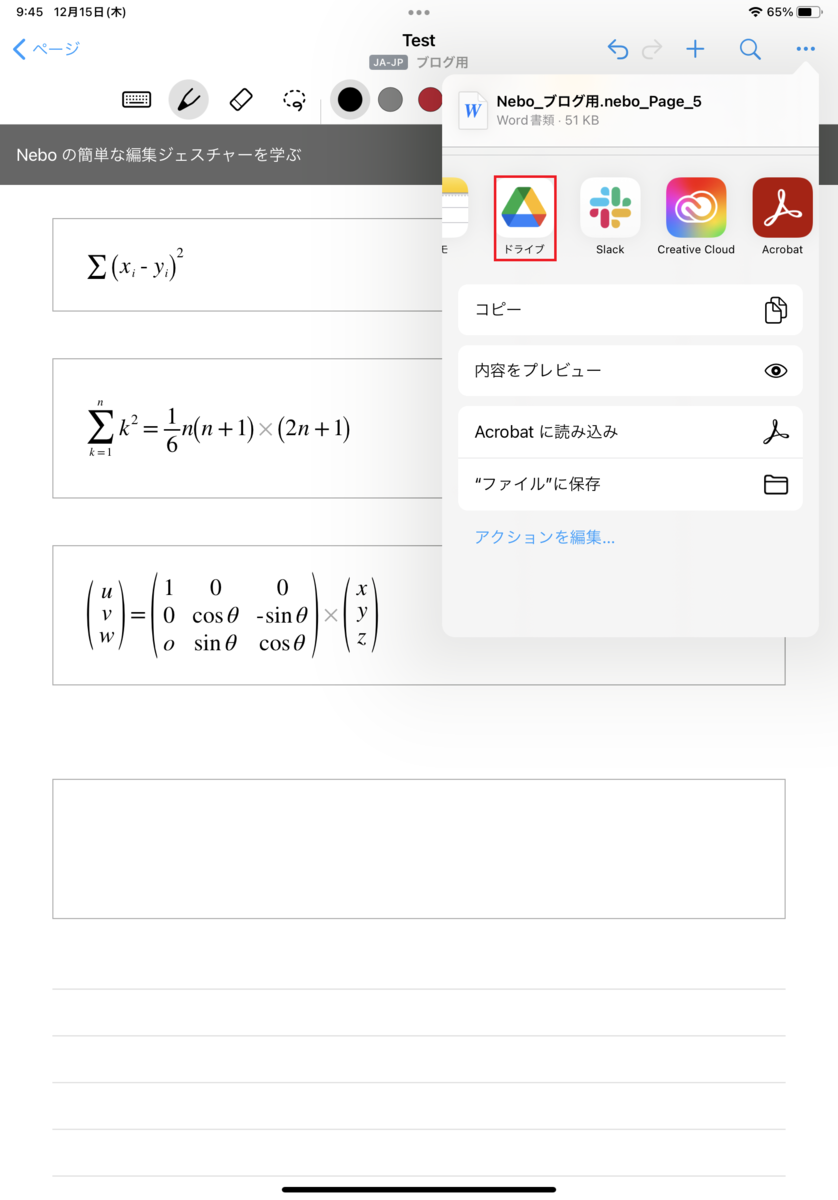
こちらの、2値化の記事の数式の例です。このように、さきほどよりも、ごちゃごちゃした式でもうまく数式に変換してくれます。
手順2 記事を執筆する
次に、MATLABを開き、livescriptにて記事を書いていきます。下の「テキスト」を押すと、文字を打つことができます。ここで、どんどん原稿を書いていくとよいです。
1でエキスポートした数式のコピペも簡単です。Wordにエキスポートしたファイルを開いてください。
右下の▼を押すと、行形式に変換することができます。その変換した数式をコピーしてください。
以下の動画は、Wordにて、さきほどのエキスポートしたファイルを開いたときの様子です。
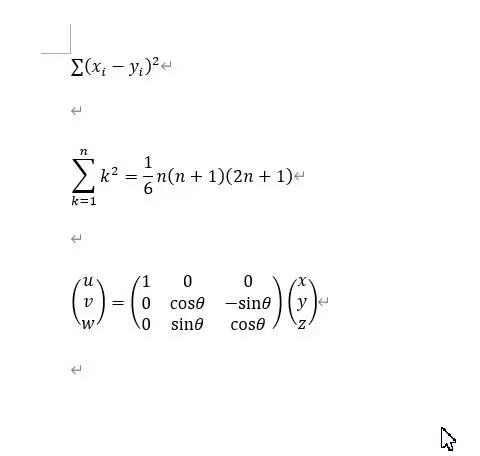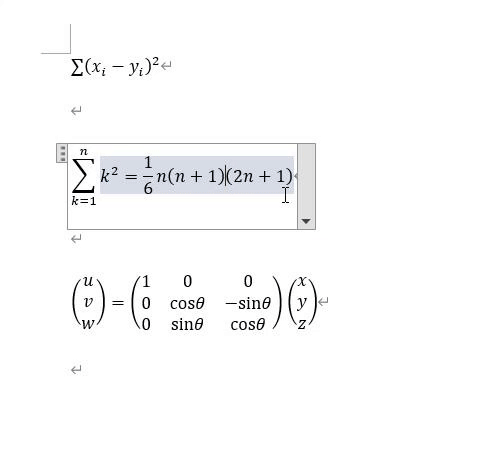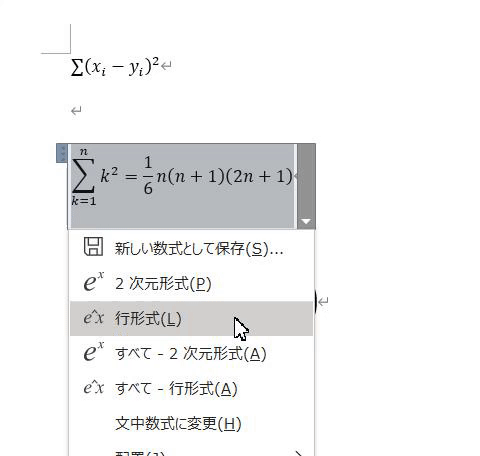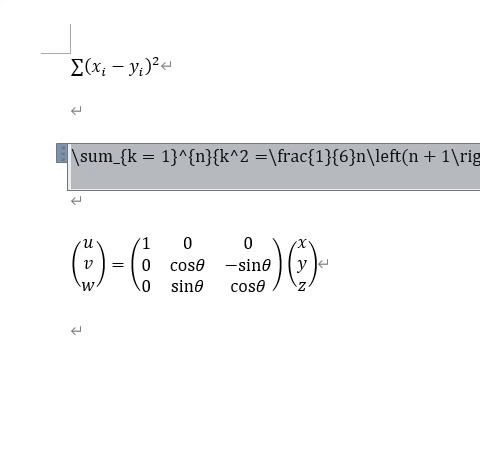
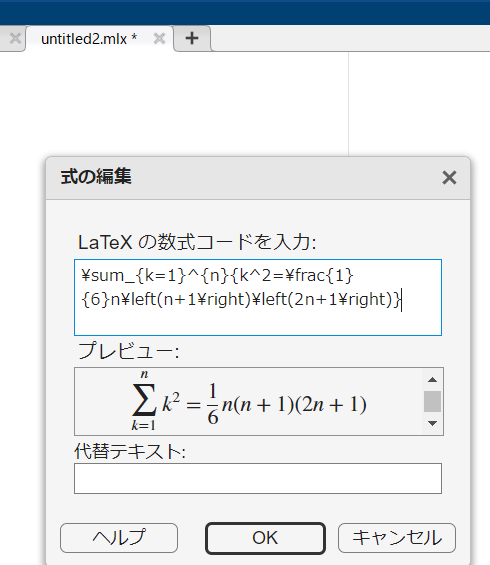
MATLABに数式をペーストするために、挿入タブ⇒式⇒LaTeX式を選択してください。
さきほどコピーした数式を張り付けると数式になります。このように数式を挿入しながら記事を書き進めます。
大変な執筆作業が終了したとします。手順3に移ります。
手順3 ブログ投稿がしやすい形で記事や画像をエキスポートする
私が普段利用している、はてなブログでは、マークダウン記法による記事の執筆が可能です。そのため、マークダウン形式でlive scriptをエキスポートすることができれば、ブログ投稿をスムーズに行うことができます。また、私は利用したことがないのですが、QiitaやZennといった他のサービスでも、マークダウン形式にて記事が執筆できるそうです。
live scriptをマークダウン形式でエキスポートするには、追加のパッケージをインストール必要があります。ホームタブ=>アドオン をクリックしてください。
以下のLive Script To Markdown Converterを検索し、インストールしてください。ボタンを押せば簡単にインストールできます。
また、githubからコードをダウンロードして、コードを実行することも可能です。
上記のアドオンがインストールできたら、コマンドウィンドウから、live scriptをマークダウン形式のファイルに変換します。コードは以下の1行で完了です。
すると、以下のようにマークダウン形式の原稿（.md）と、画像ファイルが別々でエキスポートされます。
手順4 記事を投稿する
以下の図は、さきほどのマークダウン形式のファイルをVisual Studio Code で開いたときの様子です。ここで用いるソフトウェアは他のものでも構いません。
ここでの文章を再確認しながら、はてなブログに貼り付けていきます。
プレビューモードにすると数式もうまく変換されていることがわかります。画像などを貼り付けて、その他の設定が完了すれば、投稿準備完了です。
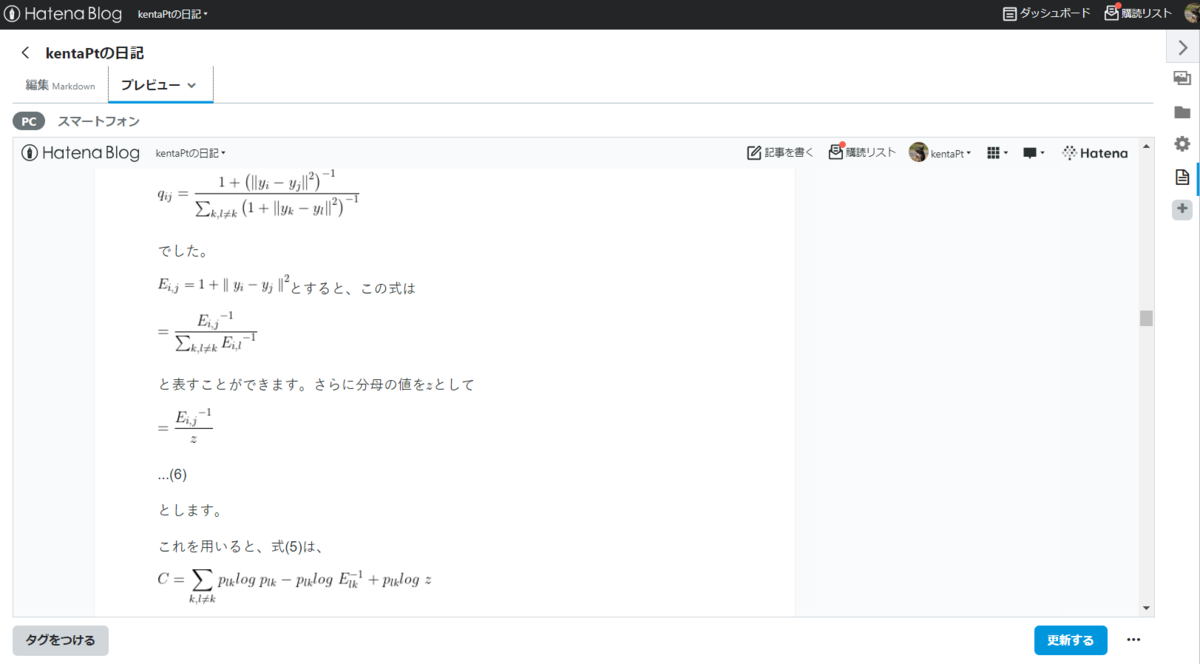
今回の方法で嬉しいこと
この章では、今回の方法でブログ記事を書いた場合に嬉しいことを述べます。あくまで個人的な意見です。また、ほかにもよりよい方法があるかもしれません。
1 初めからマークダウンで書くよりも、簡単にかける
マークダウンで書く場合は、太字にする場合や、下線を引く場合、画像を添付する場合に、それぞれの書き方があります。例えば、太字にしたい場合は、太字とし、画像を挿入したい場合は、
などとします。
個人的には、ひとつひとつこのように書いていくのは少し時間がかかってしまいます。一方、MATLABのlive scriptでは、画像は、Ctrl + V 貼り付けができ、非常に簡単です。
このような色付けも、Ctrl + M で簡単にできます。
さらに、MATLABのlive scriptでは、Wordと同様に、太字は、Ctrl + B、斜体はCtrl + IのようにWordと同じ方法で文字の調整ができます。
2 コードを書く＆実行する、と同時にブログ執筆ができる
技術関連のブログ投稿は、プログラミングコードも一緒に記述する場合が多いと思います。
私が普段行っているブログ投稿のように、技術的なことを説明しつつも、時折、コードを実行しながら理解を深める場合は、live scriptが非常に便利です。そして、ここで紹介した方法では、図（figure; plot(x, y))も一緒にエキスポートすることができます。
3 Github（Git）と連携しながら執筆できる
2と関連して、コードを書きながら記事の執筆を進める場合、間違いや、コードの修正は避けられません。一度書いたコードや原稿を、修正したあとに、「やっぱりこれがよかったな」ということはありうると思います。そのようなバックアップ用などにGit連携の機能は有用です。また、他のPCで執筆を継続する場合でも、git pullをすると、最新の状態から執筆を継続できます。
MATLAB上での操作も簡単です。
git連携については以下のページがわかりやすそうでした。
ただ、私の場合は、他の言語などを使う場合に、git bashを利用しており、
MATLABの場合も、リポジトリを作成した直後の作業では、git bashを併用しています。
注意
- iPad (nebo) =>word=>matlabでうまく数式が反映されない場合があります
- iPadにて、うまく数式が認識されない場合があります
- 私の環境では、MATLAB 2022bでは、日本語入力がやりにくいです。左上に入力した文字が表示されてしまいます。そのため、22aを利用しています
まとめ
本記事では、iPadで数式を書いて、Wordでエキスポートし、MATLABのlivescriptでブログ記事の準備をする方法について紹介しました。記事を書くのも大変な作業ですが、便利なツールを使い分けながら進めると楽しみながらできるのではないかと思います。ブログを投稿してみたい方がいらっしゃれば、その参考になれば幸いです。
先日の講演会でも、ブログ投稿のためのMATLAB利用についても質疑応答セッションで、無理やり紹介したかったのですが、時間（と関係ないことをぶっこむ勇気）が足りませんでした。アドベントカレンダーの記事として紹介できてよかったです。
サポートベクトルマシンを理解するうえで重要なカーネル法に関して勉強してみよう
この記事は、MATLABアドベントカレンダー（その2）の11日目の記事として書かれています。
本記事の執筆にあたっては、
赤穂先生の「カーネル多変量解析」を非常に参考にさせていただきました。
カーネル多変量解析―非線形データ解析の新しい展開 (シリーズ確率と情報の科学) | 赤穂 昭太郎 |本 | 通販 | Amazon
非常にわかりやすい書籍であり、大変おすすめです。
なお、本記事では、機械学習の中でも非常に有名な、サポートベクトルマシン（SVM）を理解するうえで非常に重要な手法（カーネル法）を扱います。機械学習を学習している方の参考になれば幸いです。本記事は自分の勉強のまとめであり、厳密でない記述や間違いなどあるかもしれません。その場合は教えていただけますと幸いです。
この記事の原稿や、コードは以下のページに格納されています。勉強の助けになれば幸いです。
1. はじめに
これまでの記事で、線形回帰について、詳しく述べてきました。そこで用いた図の例としては以下のようなものがあります。しかし、この例では、決定係数も約0.3とあまりうまくフィッティングすることができていません。また、次数を上げて、3次式などでフィッティングしても、ある程度の残差出てしまうことが予想されます。
上の図のような、y = ax+bで表されるような、線形的な回帰ではなく、非線形なフィッティングを考えたいと思います。
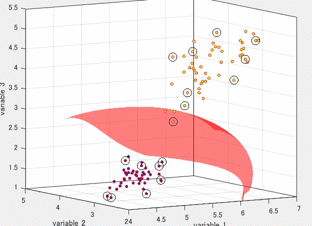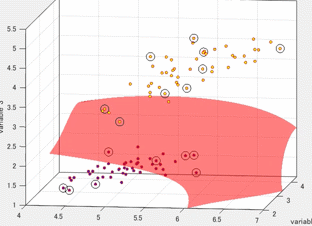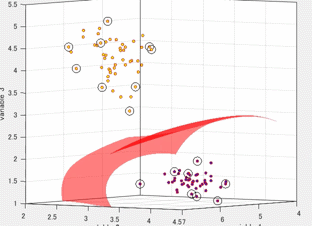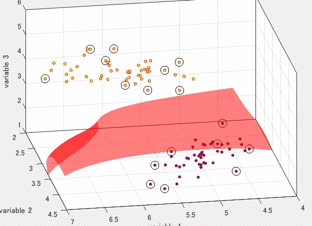
ここで、本記事にて、勉強した内容をもとに、カーネル法によるフィッティングを筆者が1から実装してみました。その結果の様子をご覧ください。
サンプルの点（青）に対して、うまくフィッティングできている（赤）ことがわかります。
さきほどの線形回帰よりも、ぐにゃぐにゃとした線でフィッティングされていることがわかります。
このような複雑な形状でフィッティングするにはどのような方法を取ればよいのでしょうか。
2章や3章にて、このフィッティングをするための式について考えていきます。
2. 線形回帰（複数の変数）を行列で表現する
2章では、以前のブログ記事で行った、線形回帰の式の導出を、行列を用いて行います。また、この場合は、変数の数が多くなっても、うまく対応することができます。
線形回帰のときは y=ax+bという式を用意し、以下のように、各yの値と、予測した値の差の2乗の値が最も小さくなるような、aとbの値を求めました。
...(2-1)
そして、これらを解くことで、以下のような、aを求める式を得ました。
...(2-2)
線形回帰については、こちらの記事をご覧ください。
この場合は、変数が1つの場合でしたが、今回は、変数がもっと多くなっても対応できるようにしたいと思います。
そのために、さきほどの線形回帰の傾きaや切片bを求めるための式を行列で書いてみることにします。
xやyは以下のようになります。これは、サンプル数が4つ（データが4件）あることを意味します。xの場合、データの値は、2、6、4、2です。
...(2-3)
yについても同様です。
...(2-4)
傾きのaについては、どのデータに対しても同じ値が用いられるため、単純に、以下のようにあらわせます。
...(2-5)
次に、変数の数が多くなった場合を考えます。y = ax1+bx2+cx3+dx4+....のような形です。
以下の式(6)の縦方向がサンプルの数、横方向が変数の次元数であるとします。
...(2-6)
例えば、以下の式を見てください。先ほどと同様にデータが4つあるとします。1つ目の変数のデータの値は、2、6、4、2です。横方向は3列ありますが、変数が3つあることを表しています。
...(2-7)
yについては、さきほどと変わりません。
...(2-8)
傾きの値は、重みとして、wで表すことにします。変数が3つあるのでそれに対応する形で、3つの要素があります。
...(2-9)
切片に相当するものはここでは考えないとすると、(2-1)式を(2-7)や(2-9)式を用いて書くと以下のようになります。
...(2-10)
i番目のデータに対して、それぞれの対応する重みを掛けて、それとi番目のyの値との差を取ります。さらにその値を2乗します。
そして、それをデータの数だけ繰り返し、足していくことで、予測値と実際の値の差の2乗の和、つまり偏差平方和を求めることができます。
これを行列で書くと以下のようになります。
...(2-11)
という所が少し分かりにくいと思います。以下に例を上げさせてください。
予測の誤差を2乗して、足すという計算が、行列の転置を使うと、簡単に表現することができます。
そして、式(2-11)の値が最小になる、重みwの値を求めたいので、wで微分をし、その値が0になる値を求めたいと思います。
...(2-12)
ここで、転置を含むときの微分の式は以下のようになります。
...(2-13)
式(2-12)と(2-13)を見比べると、
...(2-14)
...(2-15)
...(2-16)
これが0になるとき、
...(2-17)
となって、wについて解くと、
...(2-18)
となります。
このように、wについて、変数が複数ある場合でも、解析的に、誤差を最小にする重みwを求めることができることがわかりました。
3. カーネル法の利用
3.1. カーネル法を用いた時の誤差の最小化
このように、線形回帰を行うときの、重みwを求める方法はわかりましたが、この方法では、うまくフィッティングできるデータにも限りがあります。より柔軟なフィッティングができるように、カーネル法というものを導入したいと思います。
以下の例の、①や②では、足し算と引き算を行っています。別な言い方をすると、足し算や引き算をするときのルールのもと、計算しています。③でも同様に、カーネルaという筆者がここで定めた方法で計算して、その結果0という値を得ました。ちなみに、ここでは、カーネルaという計算のルールでは、2つのベクトルの内積を計算する、というふうにしました。
よく用いられるカーネルとして、ガウシアンカーネルというものがあります。その式を以下に示します。
...(3-1)
βは任意に設定できるパラメータです。の計算については以下の例をご覧ください。
要素の2乗をして、その和を取り、その平方根を求めています。つまり、
...(3-2)
としています。
この式をグラフに表すと以下のようになります。横軸は、 の値です。
さきほどの、y=ax+bのような形式は以下のように計算できました。つまり、i番目の変数に対する重みと、i番目の変数をかけ合わせ、そしてそれらの和を計算していました。
カーネル法を用いた場合も同様です。ただ、この場合は、カーネル法の計算のKの箇所が挟まります。
...(3-3)
カーネル法では、インプットしたxに対して、他の各サンプルxiとのカーネルの値に変換し、それを、重みwと掛け合わすことをしています。
例えば、サンプル数3で、変数の数（次元）が2のデータがあったとします。このデータをもとに以下のデータをテストデータとして計算する時を考えます。
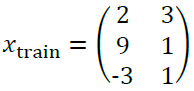
...(3-4)
テストデータは1つなので、サンプル数は1、次元は同様に2です。
そして、式3-2の
の部分では、
(2,3)と(2,8)を使って計算をして、
(9,1)と(2,8)を使って計算をして、
(-3,1)と(2,8)を使って計算をして、
それらを最終的に以下のように計算するイメージです。
数式で表すと式3-3のようになります。
そして1章で示した、線形回帰の誤差を計算するための式を再掲します。
...(1-1)
線形回帰の場合は上のような式でしたが、
同様に、カーネル法を用いた場合でも以下のように、偏差平方和を定義できます。
...(3-5)
この式を最小化する、wを求めたいと思います。
まず、その下準備を行います。
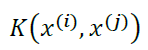
...(3-6)
は、xのi番目と、j番目の値を用いて、カーネルの値を計算するとします。
これをもとに、行列の (i, j) 成分をその値とする行列Kを準備します。つまり、
を定義します。これをグラム行列（Gram matrix）と呼びます。
グラム行列の定義や性質については以下の記事がわかりやすかったです。
ここでも同様に、
の結果を重み付けするために、
...(3-8)
を用意します。
すると、
式3-5は、
...(3-9)
と表すことができます。
ここで、線形回帰の場合は、以下の式を解きました。
...(3-12)
つまり、xがKになっただけで、同じ形になっていることがわかります。
そこで、2-18のxとKを入れ替えて、
この3-9の式が最小となる、wの値は、
...(3-10)
であることがわかります。
3.2. グラム行列の特性を生かして解き進める
ここで、2-1のように、今回は以下のようなカーネル関数を用いていました。
ここでは、aとbの値を引いて、2乗の計算をするため、aとbを入れ替えても同じ値になります。
つまり、
...(3-11)
です。
そのため、2-7からわかるように、グラム行列は
...(3-12)
を満たします。これを利用して、3-10を解き進めると、
...(3-13)
となることがわかります。
3.3. カーネル法を利用した時の誤差の和（残差平方和）について
線形回帰の場合は、誤差の二乗の和が最小となるwを選んでも、完全にそのデータに適合する直線は得られない場合がほとんどでした。そして、そのときの直線の当てはまり具合を決定係数などで評価していました。今回のようなカーネル法を利用した場合の、残差平方和はどうなるでしょうか。3-9に、 を代入します。すると、
となります。つまり、
で、カーネル法を用いてフィッティングしたときのトレーニングデータに対する
誤差はゼロとなります。
つまり、以下の図のように、青色のサンプルに対して、赤線のようにフィッティングを行うと、
与えられたサンプル全てを漏れなく通る、式を得ることができます。
3.4. 正則化項について
これまでは誤差が全くない（ゼロ）のフィッティングを行うことができることを勉強してきました。
しかし、サンプルの数（次元）が多くなるほど、そのトレーニングデータに過適合してしまいます。例えば、トレーニングデータ中にノイズの点が含まれていると、その点に引っ張られてしまいます。
つまり、トレーニングしたデータに対してはうまく行くが、それがうまくいきすぎて、逆に他の新たなデータに対しては、うまく行かないという問題が考えられます。つまり、低い汎化性が問題になります。
そこで正則化項という、このフィッティングの具合を下げるためのものを考えます。
以下のように、誤差の式にを足します。
...(3-14)
は2次形式であるため、微分の結果もシンプルになり、
となります。これにより、重みの計算もやりやすくなりそうです。
また、この微分に関しては、さきほどの、1-13式に、c=0, d=0, A=λ, B=Kを代入しても同じ結果が得られます。
...(2-13)
という項が入ると、さきほどのように、トレーニングデータに対して、完全にフィッティングすることはできません。しかし、それにより、トレーニングデータに過剰に適合することを抑えることができます。
3-14を微分して、
...(3-15)
この値が0になるときは、以下の式を満たす。
...(3-16)
...(3-17)
...(3-18)
このような重みwを選ぶことで、トレーニングデータに過適合しないようなフィッティング結果が得られます。しかし、この正則化の程度をコントロールする、係数λを適切に選ぶ必要があります。
3.5. カーネルについてもう少し考えてみる
先ほどは、カーネルの関数として、ガウシアンカーネルを利用しました。
（これがカーネルとして利用できるかは置いておいて）、以下のような関数をカーネルとして選んだとします。
...(3-19)
すると、以下のように6次元のベクトルの内積として書き換えることができます。
なお、この節での説明は以下のページを参考にさせていただきました。
How to intuitively explain what a kernel is?
機械学習に詳しくなりたいブログ
カーネルとは直感的に説明するとなんなのか？
次に、ガウシアンカーネルについて、同様に、n次元のベクトルの内積に書き換えられないかを考えてみます。
ガウシアンカーネルは以下のように定義されていました。
ここで、
とおきます。これをテーラー展開 (Taylor expansion)すると以下のようになります。
...(3-20)
ガウシアンカーネルも、無限次元のベクトルの内積に書き換えられる気がしてきました。
ここから、ガウシアンカーネルを無次元特徴量として表すための、式展開は、以下のようになります。
なお、この式展開については、
佐久間淳先生 機械学習(6)カーネル/確率的識別モデル1の講義資料をそのまま掲載させていただいております。
非常にわかりやすい資料を公開していただき、ありがとうございました。
https://ocw.tsukuba.ac.jp/wp/wp-content/uploads/2019/10/e279a56fc6a000e67d6370309f9374c1.pdf
このように、ガウシアンカーネルを用いた時は、無限次元の特徴量を計算していることと等しいです。
次元が無限だけあるので、これを全て1からコツコツ計算していくことは、（真正面から計算する場合は）できません。
しかし、ガウシアンカーネルを用いた上の計算をすると、この無限次元の計算をした場合と等価になります。
このようにカーネルとして利用できる関数をもってくれば，無限次元の特徴ベクトルの内積を非常に簡単に計算できます。これは「カーネルトリック」と呼ばれています。
4. カーネル法を用いたフィッティングを実装してみよう
冒頭で述べた通り、4章で用いたコードは以下のページにアップロードされています。
4.1. 正則化項を使用しない場合
3章までは、カーネル法を用いたフィッティングを行うことで、線形回帰よりもはるかに柔軟性のあるフィッティングを行うことができることを示してきました。4章では、これまでの理解を確認および定着させるために、実際にそれらをコーデイングして、うまくいくか確認してみたいと思います。
言語はMATLABを用いました。3章までの数式をもとに実装しました。いったん数式を解いてしまえば、比較的短い行で書くことができました。正則化項を使用しない場合は、上で説明したとおり、サンプルデータに完全にフィットする結果を得ることができました。
clear;clc;close all %% パラメータ設定 % ガウシアンカーネル中のベータの値 beta = 1; % 正則化のパラメータ L2regu = 0; %% サンプルデータの作成と計算の準備 rng('default') % For reproducibility x_observed = linspace(0,10,21)'; y_observed1 = x_observed.*sin(x_observed); y_observed2 = y_observed1 + 0.5*randn(size(x_observed)); numSample = numel(x_observed); K = zeros(numSample, numSample); %% グラム行列の計算 % わかりやすくfor文を2つ用いて実装します for i =1:numSample for j = 1:numSample diff = (x_observed(i)-x_observed(j))^2; K(i,j) = exp(-beta*diff); end end %% 重みwの計算 w = inv((K+L2regu*eye(numSample)))*y_observed2; %% 結果の可視化 % サンプルデータのプロット figure;scatter(x_observed,y_observed2);hold on % フィッティングした結果のプロット numSample_test = 100; x_test = linspace(0,10,numSample_test)'; kOut = zeros(numSample_test,1); for i =1:numSample_test x_i = x_test(i); diff_test = (x_observed-x_i).^2; kOut(i) = w'*exp(-diff_test.*beta); end plot(x_test,kOut) title(sprintf('L2正則化の係数=%d',L2regu));hold off
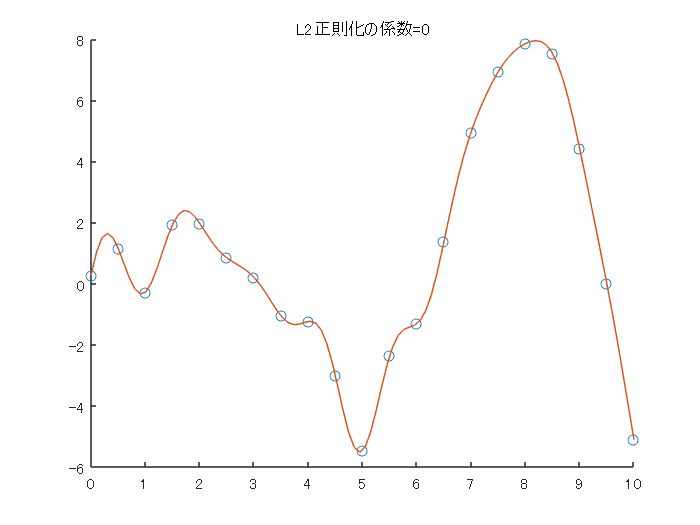
4.2. 正則化項を変えながら実行する
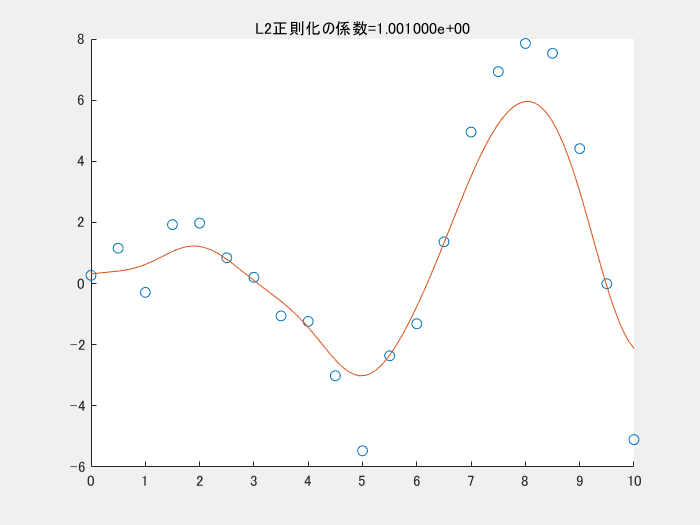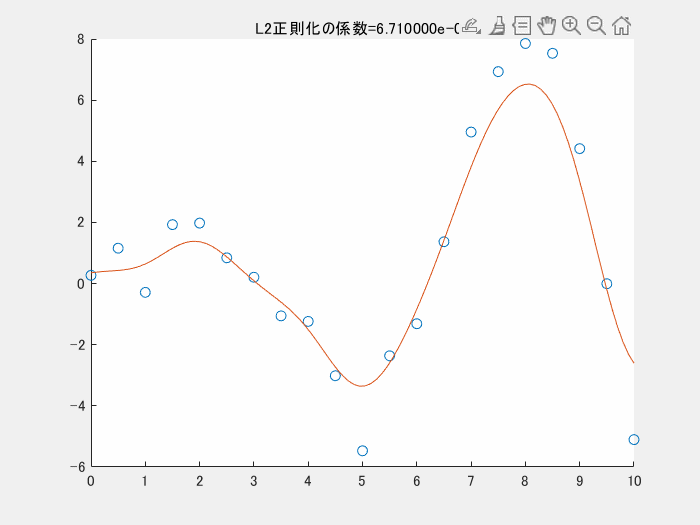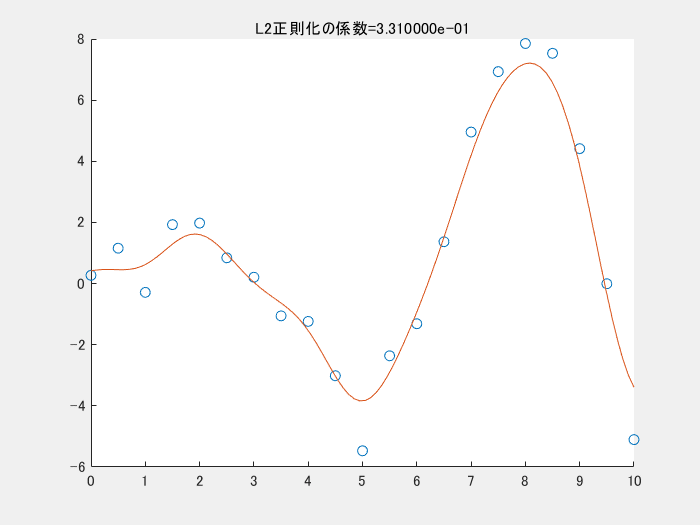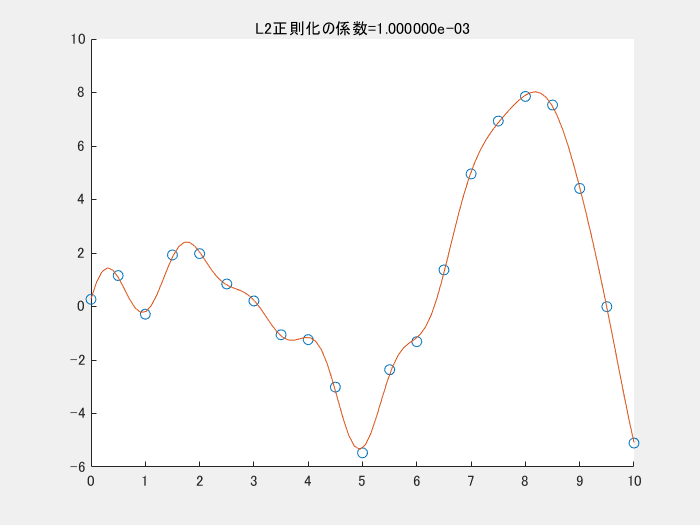
4.1では、正則化項を利用しませんでした。以下の図は、正則化項のパラメータを変えながら実行した時の様子です。この図のコードもgithubにアップロードしています。正則化項の係数が小さくなる（影響を小さくする）と、真ん中下の、急に値が小さくなっている点にも適合しようと、曲線全体がより複雑になっていることがわかります。
5. まとめ
- カーネル法を用いたフィッティングの方法についてまとめました
- トレーニングデータに対して、誤差のない、複雑な曲線を描くことができます
- 自身の手でも実装し、勉強したとおりのフィッティングができることを確認しました
- 機械学習において、非常に有名な、サポートベクトルマシンを理解するうえで非常に重要なトピックを扱いました。サポートベクトルマシンを学習しているかたの参考になれば幸いです。
参考ページ（本文中に記載のないもの）
線形な手法とカーネル法（回帰分析）
t-SNEの勉強メモ
この記事は、MATLAB/Simulink Advent Calendar 2022の6日目の記事として書かれています。
1章 はじめに
t-SNEと呼ばれる方法を用いて、高次元データを、2次元平面や3次元空間にプロットすることができます。
例えば、以下の図は、MNISTという0から9の手書き数字の画像の情報を2次元平面にプロットしたときの様子です。
0から9の画像のサンプルデータが、それぞれクラスタを形成しており、うまく可視化できていることがわかります。
PCA (主成分分析)と呼ばれる方法を用いて、次元圧縮を行い、上のような2次元や3次元上でのプロットを得ることもできます。しかし、主成分分析では、高次元空間上で線形的な構造を有しているものに対して、有効であり、非線形な構造を有しているデータに対しては、うまく低次元空間にマッピングできないという欠点があります。主成分分析については、以下の私の過去の記事をご覧ください。
本記事の執筆においては、以下のページを参考にさせていただきました。ありがとうございました。
t-SNE 解説
Parametric t-SNEの理論とKerasによる実装
t-SNE を用いた次元圧縮方法のご紹介
この記事では、初めにt-SNEについて簡単にまとめ、その後、パラメータをいくつか変えながらt-SNEについて勉強していこうと思います。
なお、この記事の原稿やコードは以下のページにて公開されています。
2章 t-SNEについての自分用まとめ
ここからは、t-SNEの処理の流れについておおまかにまとめていきます。より正しい/詳しい解説にて勉強したい方は上の参考ページをご覧ください。
2.1. t-SNEの目標
n次元上に複数の点が存在するといます。その空間上の任意の点のペアを作り、それらを2次元平面（や3次元空間）に写像したときのことを考えます。
(i) 近い点：2次元平面（や3次元空間）に点を写像したときも、それらの点が近いままにする
(ii) 遠い点：2次元平面（や3次元空間）に点を写像したときも、それらの点が遠いままにする
(i) (ii)のように、高次元と低次元空間上で、それらの点の近さの関係をできるだけ保つようにしていきます。まずは、2.2で、この近さについてどのように定義していくかについて述べていきます。
2.2. 近さ（類似度）の定義について
2.2.1. 高い次元の場合
高い次元の空間（高次元空間）での任意の点どうしの距離を、正規分布に従う確率分布でモデル化します。
はじめに、正規分布の確率密度関数の式は以下のように表すことができます。
...(1)
そもそも、なぜ確率密度関数の式がこのようになるのか、ということについては、以下のページがわかりやすかったです。
ここで、2つの点、 と
を考えます。先ほどの、正規分布の確率密度関数の式をもとに、以下のように近さ（類似度）を表してみます。
直感的には、分母で、全てのペアの距離を足して、それで割ることで正規化しています。確率密度関数の式のexpの直前の値は、分母分子で共通しているのでキャンセルされています。
...(2)
はユーザーの指定する必要があります。
上で定義した近さについては、SNEと呼ばれる、t-SNEのもととなった手法での近さを示しています。t-SNEでは、近さを以下のように定義します。
はデータ数を示します。
そのため、t-SNEにおいては、
であると言うことができます。ひとまず、高次元空間の任意の点の距離を正規分布の確率密度関数の式をもとに、定義しました。
2.2.2. 低い次元の場合
低次元空間上の類似度を以下のStudentのt-分布(自由度1)で表現します
...(3)
ここで、t分布の一般式は以下のとおりです。
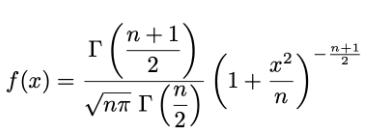
を含まない部分は、分母と分子で共通するためキャンセルされます。残った
には1を代入し、
に
を代入すると上の式になることがわかります。
高次元空間上では、正規分布を使った一方で、ここでは、t分布を用いています。その理由については、Crowing problemがあるそうです。元の論文にも記述されていますが、以下のブログの解説がわかりやすかったです。
2.3. 高次元空間上の点を低次元空間上に写像するときの考え方
高次元空間上および写像後の点の近さ（遠さ）を保てるようにするため、KLダイバージェンスを用います。
KLダイバージェンスを用いた損失関数としては、以下のようなものを用います。
....(4)
ここでは、点 i と点 jの、高次元空間と低次元空間上の距離が似ている（割り算すると1になる）ほど、logの中身が1に近づきます。それにより、式(4)の値自体も0に近づきます。
勾配法によって、低次元空間に写像する点を少しずつ変化させていき、KLダイバージェンスの値をどんどん小さくしていきます。
2.4. KLダイバージェンスの式の微分について
式(4)で示した、KLダイバージェンスの式を微分していきます。
先ほど示したような、以下の式を微分するために、logの中身を展開していきます。
...(5)
ここで、式(3)の通り、
でした。
とすると、この式は
と表すことができます。さらに分母の値をとして
...(6)
とします。
これを用いると、式(5)は、
...(7)
と書き換えることができます。低次元空間上にマッピングしたときの値であるを求めるために、
低次元空間上のについて微分を行う。
...(8)
第一項目は、yが含まれないため、0となる。
この式(8)の2項目について考える。
および
であることから、
ここで、
...(9)
とすることができる。
さらに、
なので、
（以下、式どうしに説明があったりして、スキャンした画像のまま掲載させてください）
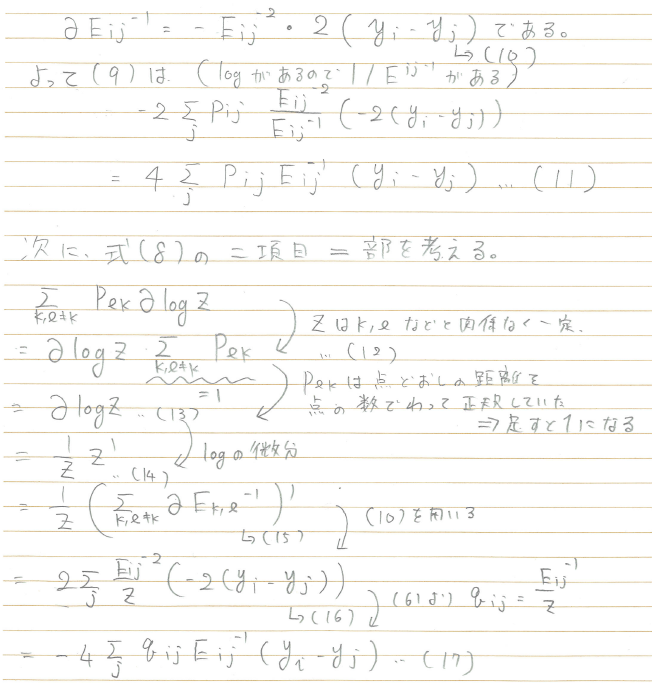
（スキャンした画像終わり）
(11)および(17)で計算した、(8)の第一項と第二項を足し合わせると、
...(18)
を得ることができる。
...(19)
となり、で微分すると、このようにきれいな式を得ることができました。
この式をもとに勾配法などで更新していくことで、2次元平面や3次元空間上に写像したの座標を求めることができます。
3章 t-SNEで遊んでみよう
この章では、2章で簡単にまとめた、t-SNEいろいろ試してみたいと思います。以下の公式ドキュメントを参考にします。
3.1. データのダウンロード
以下の、THE MNIST DATABASE of handwritten digitsにあるデータをダウンロードします。以下のページにアクセスしてください。手書き数字のデータセットをダウンロードすることができます。以下の左下の赤枠をご覧ください。
以下のようなtrain-からはじまるファイルを2つダウンロードしてください。そして、7zipなどを用いて、ダウンロードした gz ファイルを解凍します。すると、以下のように-ubyteで終わるファイルを2つ得ることができます。
imageFileName = 'train-images.idx3-ubyte'; labelFileName = 'train-labels.idx1-ubyte';
processMNISTdata.mというコードを用いて、t-SNEによる解析を行うための前準備を行います。
[X,L] = processMNISTdata(imageFileName,labelFileName);
Read MNIST image data... Number of images in the dataset: 60000 ... Each image is of 28 by 28 pixels... The image data is read to a matrix of dimensions: 60000 by 784... End of reading image data. Read MNIST label data... Number of labels in the dataset: 60000 ... The label data is read to a matrix of dimensions: 60000 by 1... End of reading label data.
計算時間短縮のため、以下のコードでサンプルを減らします。必要なければ、===で囲まれた範囲をコメントアウトしてください
% ============= idx = randperm(numel(L),round(numel(L)*0.1)); X = X (idx,:); L = L(idx); % =============
画像がどのようなものか確認します。以下のように手書き数字のデータセットであることが確認できます。
dispIdx = randperm(numel(L),9); dispCell = cell(9,1); for i=1:9 X_i = X(dispIdx(i),:); dispCell{i} = reshape(X_i,[28 28]); end figure;montage(dispCell)
3.2 t-SNEによる次元圧縮
さっとく、さきほどの手書き数字のデータセットをt-SNEを用いて解析し、2次元平面にデータをプロットしたいと思います。t-SNE関数を用いて簡単に実行することができます。
- Barnes-Hutアルゴリズムを用いて、大規模なデータを効率的に処理します
- 主成分分析（PCA）を用いて、次元を784から50に削減してから、t-SNEを実行します。主成分分析については、以下の私の過去の記事をご覧ください。
rng default % for reproducibility % t-SNEの実行時間を計測 tim = tic; Y = tsne(X,'Algorithm','barneshut','NumPCAComponents',50,'Perplexity',30); toc(tim)
経過時間は 176.732598 秒です。
numGroups = length(unique(L)); % クラス数に従い、色を定義 clr = hsv(numGroups); % 可視化 figure;gscatter(Y(:,1),Y(:,2),L,clr);title('Default Figure')
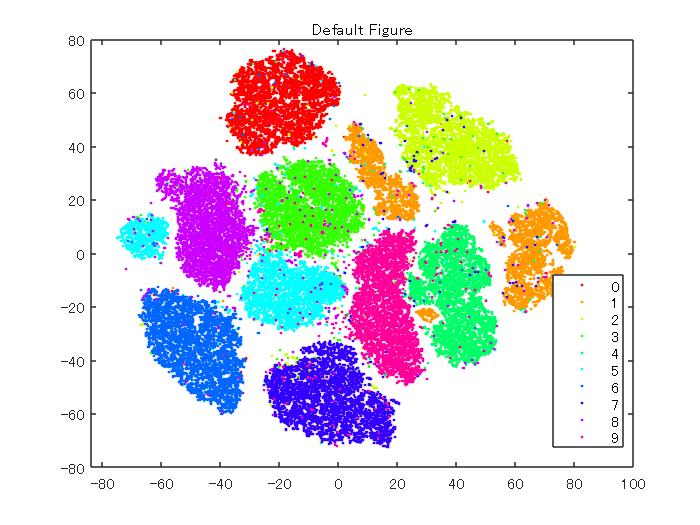
t-SNEを用いて、各数字をクラスタに分けることができました。比較的、ミスしている点も少なく、きれいに可視化できていることがわかります。
3.3. パラメータの変更
3.3.1. Perplexityについて
以下のように、Perplexityの値を変更していきます。パープレキシティが大きくなると、tsne はより多くの点を最近傍として使用します。データセットが大きい場合は、Perplexity の値を大きくします。一般的な Perplexity の値の範囲は、5 ～ 50 だそうです。
rng default % for fair comparison Y50 = tsne(X,'Algorithm','barneshut','NumPCAComponents',50,'Perplexity',50); figure gscatter(Y50(:,1),Y50(:,2),L,clr) title('Perplexity 50')
rng default % for fair comparison Y4 = tsne(X,'Algorithm','barneshut','NumPCAComponents',50,'Perplexity',4); figure gscatter(Y4(:,1),Y4(:,2),L,clr) title('Perplexity 4')
perplexityを50に設定した場合は、比較的、はじめの図と似ていると思います。一方、4にすると、各クラスターが込み合ったような図になっています。
3.3.2. Learning Rate（学習率）について
次に、学習率を変えて比較したいと思います。
以下のコマンドでは、学習率を5に設定します。
rng default % for fair comparison
YL5 = tsne(X,'Algorithm','barneshut','NumPCAComponents',50,'LearnRate',5);
figure
gscatter(YL5(:,1),YL5(:,2),L,clr)
title('Learning Rate 5')
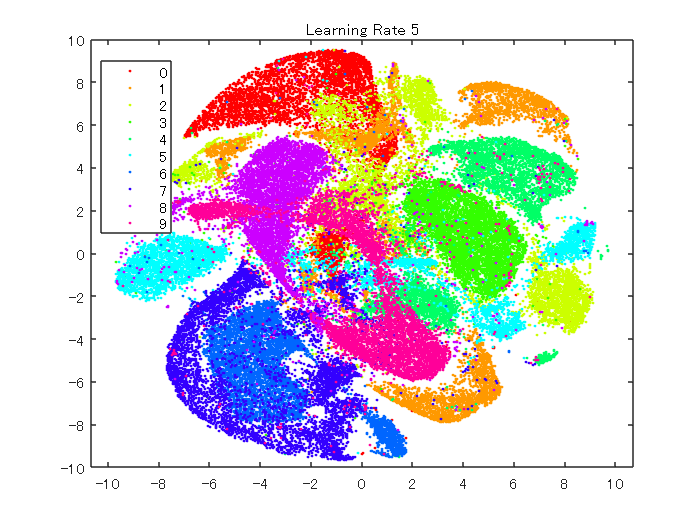
次に学習率を2000に設定します。
rng default % for fair comparison YL2000 = tsne(X,'Algorithm','barneshut','NumPCAComponents',50,'LearnRate',2000); figure gscatter(YL2000(:,1),YL2000(:,2),L,clr) title('Learning Rate 2000')
以上のように、学習率を変えると、また異なる結果を得ることができました。データによるため一概には言えませんが、学習率が小さすぎると、最適な解にたどり着けず、十分分離されていない結果が得られると思います。一方、大きすぎても、最適な場所に解が落ち着かないため、きれいな分離結果を得ることができません。
4章 簡単なまとめと注意点
簡単なまとめ
この記事では、t-SNEの仕組みを簡単に説明し、さらにMATLABを用いて、その動作を確認しました。Perplexityや学習率などのパラメータがあり、それらの設定によって結果が異なることがわかりました。
その結果を使用して新しいデータを分類することはできない
多くの場合に t-SNE はデータをクラスターにきれいに分離するので、新しい手元のデータにも試したくなります。しかし、t-SNE は新しいデータ点をクラスターに分類できません。t-SNEによるマッピングは、データに依存する非線形写像で、新たに低次元空間に新しい点を埋め込むためには再度その点を含めてt-SNEを実行しなおす必要があります。一方主成分分析（PCA）による方法では、マッピングするための重みなどが求まるため、新たなデータに対しても適用することができます。
参考ページ（本文中に記載のないもの）
1 Yann LeCun (Courant Institute, NYU) and Corinna Cortes (Google Labs, New York) hold the copyright of MNIST dataset, which is a derivative work from original NIST datasets. MNIST dataset is made available under the terms of the Creative Commons Attribution-Share Alike 3.0 license
2 MATLABドキュメンテーション：t-SNEとは
3 Federico Errica: Step-By-Step Derivation of SNE and t-SNE gradients
線形回帰（単回帰分析）を1から実装して理解を深めてみよう: つづき
この記事は、MATLABアドベントカレンダー（その2）の5日目の記事として書かれています。
1 はじめに
前回の記事では、以下のように、線形回帰（単回帰分析）を行った時の、式の傾きや切片の求め方についてまとめました。
例えば、以下の図では、y = 0.33x + 50.2 という式が得られています。この傾きや切片を、xとyのペアからどのように求めるか、ということでした。
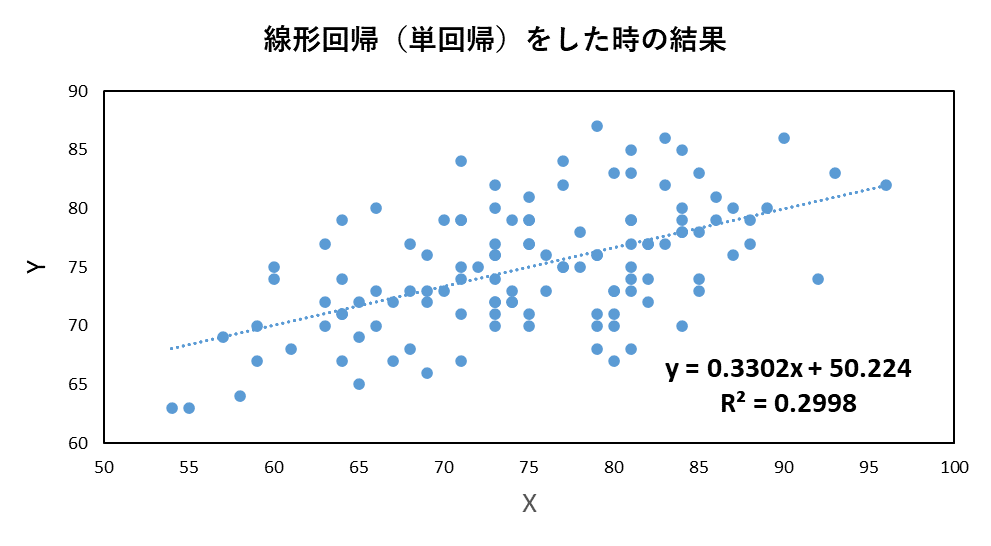
具体的には、傾きは、
...(前回の記事の17)
であり、切片については以下の通りでした。
...(前回の記事の18)
しかし、文量が多くなってしまい、上の図中にあるような、決定係数 の求めかたについては、触れられていませんでした。
そこで、本記事では、線形回帰（単回帰分析）をしたときの、決定係数の求め方について、簡単にまとめます。さらに、MATLABを用いてコーディングをし、ここでの理解による実装の結果と、MATLABのregress関数およびExcelの結果が一致することを確かめます。
本記事は、タイプミスや間違いなどがあるかもしれません。その場合教えていただけますと幸いです。
2 決定係数の求め方について
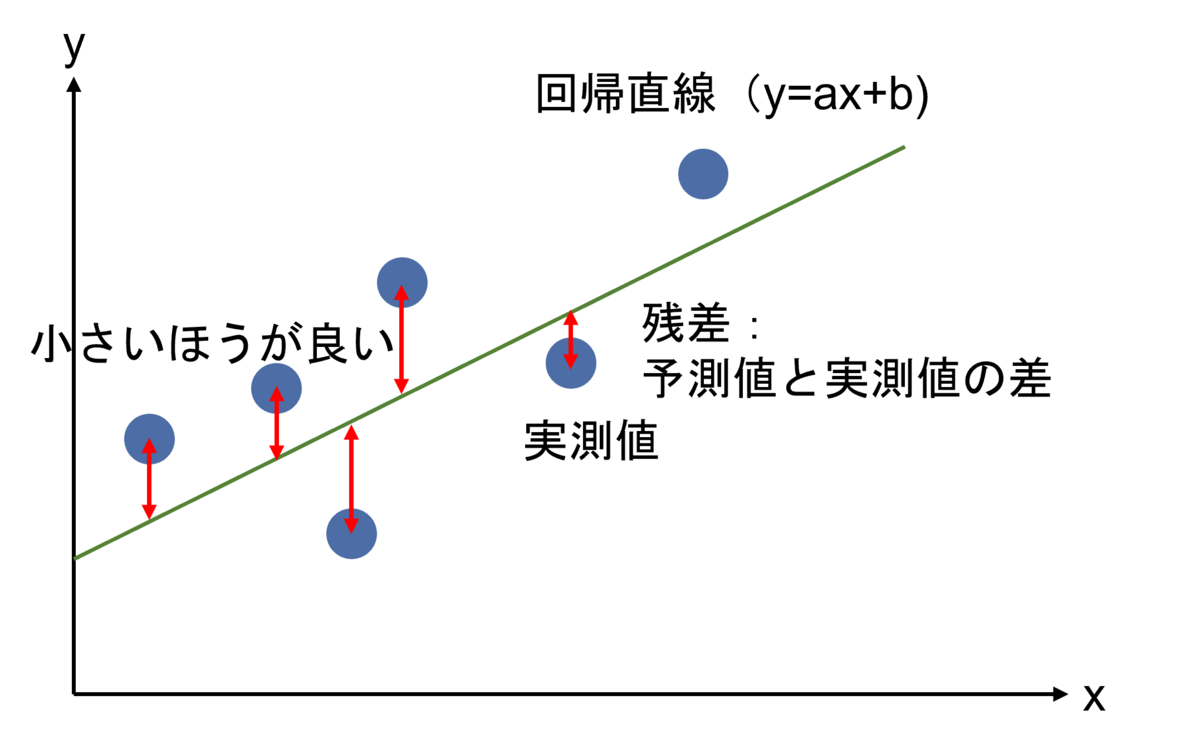
決定係数は、以下の図の、残差を利用して求めることができます。残差とは、予測値と実測値の差のことです。
この値が小さければ小さいほど、決定係数は高くなりそうです。では、具体的にどのような式で決定係数を求めるのか見ていきたいと思います。
回帰分析における寄与率(=決定係数)と、残差や相関係数との関係を参考に作成
2.1. 偏差積和を用いた傾きと切片の式の展開
2.1.1. 傾きについて
以下のような、偏差積和を考えます。はxの平均です。yについても同様です。
各サンプルから、そのを引き算し、yについても同様の処理を行ったものとの積を求めます。それをサンプル全体に対して行い、和を取ります。
...(1)
偏差積和についてはより詳しい内容を知りたい方は以下のページをご覧ください。
https://toukeigaku-jouhou.info/2017/06/24/variance-covariance/
(1)の中身を展開して、
...(2)
各項にばらして、
...(3)
xの和は、xの平均と個数を掛け合わせたものと等しいので、
...(4)
...(5)
となります。
Σの中に戻して、
...(6)
を得ます。
傾きの式の分子に相当することがわかります。
...(前回の記事の17)
次に、aの式の分母について考えます。
式(1)において、x = y であるとします。すると以下の等式が成り立ちます。
...(7)
式を整理すると、
...(8)
となります。この左辺の式はaの分母と等しいことがわかります。
そのため、aは以下のように書き換えることができます。
...(9)
偏差積和をのように表すとすると、
...(10)
のように表せます。
さらに、偏差積和をサンプル数で割ると、共分散になるため、
...(11)
...(12)
とすることができます。ここでは、共分散をのように表しています。
なお、式(10)から(12)にて扱ったような、共分散については以下のページがわかりやすかったです。
共分散の意味と簡単な求め方
2.1.2. 切片について
切片は以下のようになるのでした。
...(前回の記事の14)
aにさきほどの式(12)の結果を代入します。
...(13)
一項目と二項目を入れ替えます。
...(14)
という関係であるため、
...(15)
であることが言えます。
これにより、傾きと切片の式がかなり見やすくなりました。
決定係数を求めるために、最後の準備を行います。
2.2. 平方和の分解
y = ax+bの式では、xが大きくなるほど、yの値もaxだけ大きくなります。もし、この回帰式が完全である場合、yの変動は、xの変動によって
完全にカバーすることができます。しかし、実際は、ノイズなどの影響で、完全な式は得られることはなく、そのxの変動では説明できない部分が発生してしまいます。この説明できない部分が小さいほどうれしいです。では、このxの変動によって説明される部分と、説明されない部分をどのように切り分けるとよいでしょうか。
はじめに、
の平均回りの変動（平方和 ）は、説明変数
の変動によって説明される部分と、説明できない残差の平方和に分解することができます。
実際に計算していきます。 の平均回りの変動（平方和 ）は以下の通りです。
...(16)
y = ax+bという式で回帰しているため以下のように記述できます。
...(17)
展開して、
...(18-1)
ここで、式(18)の3つ目の項について考えます。
...(18-2)
前回の記事で、回帰残差の和はゼロになることを確かめました。
つまり、残差を以下のように定義したとします。
...(19-1)
すると、
...(19-2)
が成り立ちます。
さらに、同様に前回の記事で、
回帰残差とxの値はベクトルとして直交していることも確かめました。
そのため、式(18)は、
...(19-3)
であることがわかります。そのため、この値は0になるため、式から除外します。
式(18-1)は以下のようになります。
...(19-4)
さらに、式(19-4)の1項目について考えます。
...(20)
同様に、前回の記事で、推定された回帰直線は、サンプルのxとyの平均を通ることを確かめました。
そのため、式(20)は以下のように書き換えることができます。
...(21)
この式を展開して、
...(22)
第三項目のを１つだけ展開します。
であることを上で確かめました。そのため、
...(23)
であり、二項目と三項目を計算できます。
...(24)
この式の左辺の値（残差平方和）である、を
F
とします。
すると、
...(25)
とすることができます。とすると、
...(26)
です。
ここで、以下の式がもとになっていました。
...(19-4を再掲）
そして、
をとした場合、
である関係式を得ました。
この関係式を19に代入すると、
...(27)
であり、
...(28)
となります。
ここで、と置いていました。
式(12)より、
...(29)
です。
2.3. 決定係数の式の定義
式(26)を振り返ってみます。 としたときの、
は、目的変数yを二乗して足し合わせたもので、全変動を表しています。
また、は残差平方和でした。つまり、（全変動）＝（残差平方和）＋
となっており、はデータの変動のうち、回帰直線によって表すことのできる量であると考えることができます。
そこで、決定係数を、全変動のうち、回帰直線によって表すことのできる割合であるとし、大きい（最大1）ほどよいものになります。
式で表すと、
...(30)
となります。式(26)を利用して、
...(31)
となります。
これにより、決定係数を計算するための式を得ることができました。
2.4. 決定係数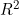
と相関係数rの関係
式(30)を以下のように変形します。
相関係数は、xとyの共分散であるをxとyの標準偏差で割ったものであるため、
...(32)
このような関係式を得ることができました。単回帰分析の場合は、相関係数を2乗とすると決定係数になることがわかりました。
相関係数については、以下のページがわかりやすかったです。
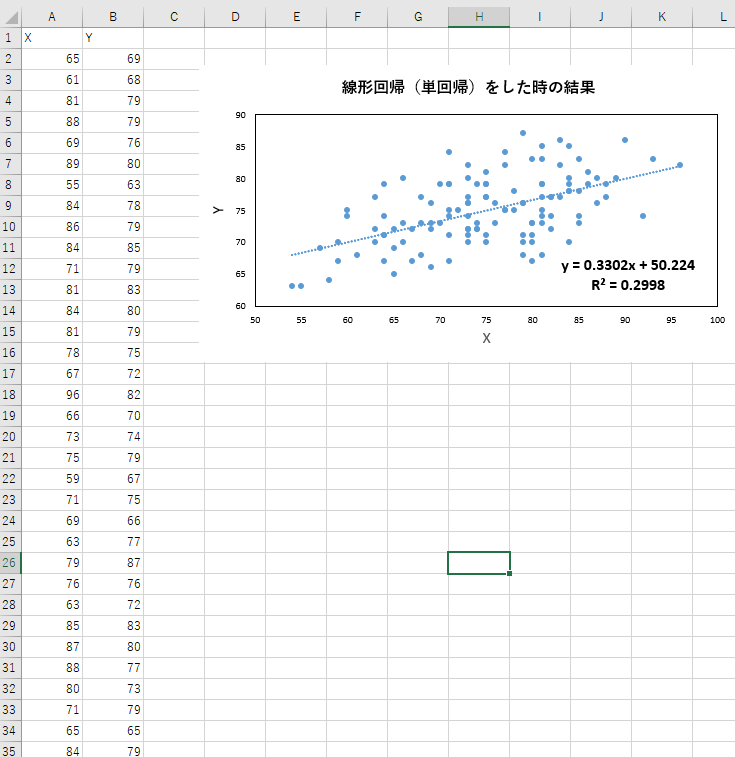
3. MATLABとExcelを用いて、2章の決定係数の式が正しいか確認してみよう
ここで、2章の結果が正しいかどうかを、実際にコーディングして確かめてみます。以下の3つの結果が同じになるかを検証します。
3.1. MATLABのregress関数にて、単回帰分析を行った場合の決定係数の値
load examgrades
yとXの値を設定します。
y = grades(:,5); X = [ones(size(grades(:,1))) grades(:,1)];
regress関数で単回帰分析を行います。決定係数は0.2998でした。
[mdl,~,r,rint,stats] = regress(y,X); disp(strcat('R2_MATLAB= ',string(stats(1))))
R^2=0.2998
3.2. Excelにて、単回帰分析を行った場合の決定係数の値
3.1にて用いたデータをコピーアンドペーストして、「近似曲線」の機能を用いて、
傾きと切片の値を計算しました。
3.1と同じ、決定係数の値が計算されており、まずは、3.1および3.2で、ソフトウェアの関数や機能にてうまく値が計算できたと思われます。
3.3. MATLABにて2章の結果を1から書いて計算させたときの決定係数の値
前回の記事で得た、
...(前回の記事の17)
および
...(前回の記事の18)
を用いてまずは、傾きと切片の値を計算します。
さらに、(30)のの値を計算します。
x = grades(:,1); bunshi_a = sum(x.*y)-1/numel(x)*sum(x)*sum(y); bumbo_a = sum(x.^2)-1/numel(x)*(sum(x)^2); a = bunshi_a/bumbo_a; b = -1/numel(x)*sum(x)*a+1/numel(x)*sum(y); SR = sum((a*x+b-mean(y)).^2); Syy = sum((y-mean(y)).^2); R2 = SR/Syy
R2 = 0.2998
こちらも0.2988になり、正しいことがわかりました。
これらの結果から、2章の私の理解や、ここでのコーディングはおおよそ正しそうです。
4. 簡単なまとめ
- この記事では、線形回帰（単回帰分析）における、決定係数の計算方法についてまとめました。
- MATLABとExcelを用いて、ここでまとめた決定係数の式が正しいことを確認しました
- 普段から何気なく使っている決定係数ですが、丁寧に求めて記事にまとめるのが大変でした。しかし、これまでより広い視点で線形回帰を使えそうな気がしました。
- （全変動）＝（残差平方和）＋（データの変動のうち、回帰直線によって表すことのできる量）という関係式を求め、決定係数の計算をしました。しかし、この式の導出は飛ばして、公式のような形で決定係数の定義を覚えて、決定係数の計算をしてしまってもいいかもしれません（？）
5. 参考文献（本文中に記載のないもの）
回帰直線の式を最小二乗法により計算する
永田靖、棟近雅彦共著：多変量解析入門
線形回帰（単回帰分析）を1から実装して理解を深めてみよう
この記事は、MATLABアドベントカレンダー（その2）の4日目の記事として書かれています。
1 はじめに
以下の図のように、エクセルなどで、直線で回帰（フィッティング）した経験がある方も多いかもしれません。
以下の図では、y = 0.33x + 50.2 という式が得られています。
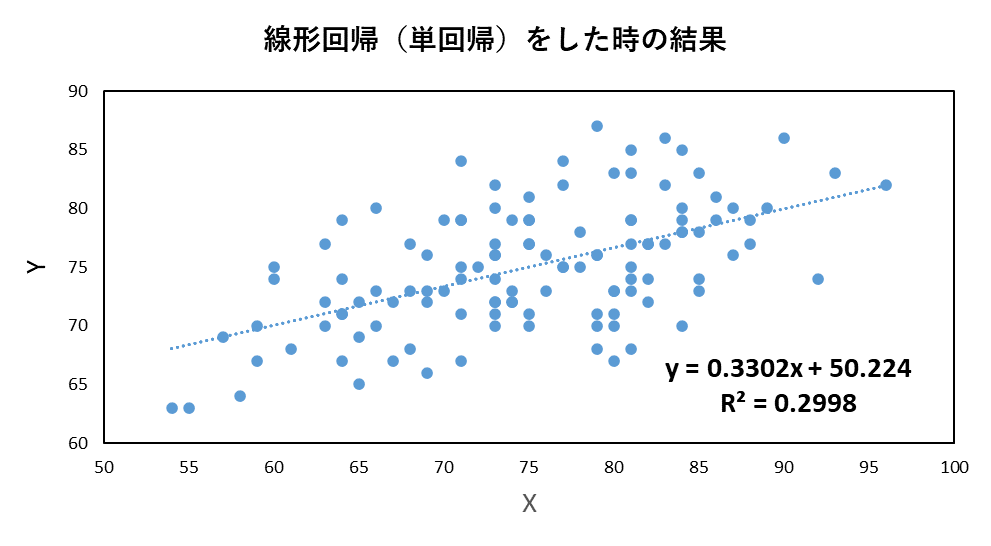
例えば、これにより、データ同士の相関関係を知ることができ、非常によく用いられる解析方法です。
このような線形回帰（単回帰）の説明としては、以下のページがわかりやすかったです。
回帰分析(単回帰分析)をわかりやすく徹底解説！
実は簡単！ 10分あれば回帰分析ができます
よく用いられる手法ではありますが、それを実際に、導出し、自分の手で（プログラミングやExcelを使って）検算したことのある人は、
あまり多くないかもしれません。ここでは、自分の勉強のまとめとして、線形回帰の中でも、1つの変数を用いた、単回帰の導出を行い、さらに、複数の方法での実装（プログラミング）により自身の理解が正しいことを確認します。なお、実装による確認などを通して、検算はしていますが、間違いなどあるかもしれません。その場合は教えていただけますと幸いです。
この記事の原稿や、コード、検算用のExcelファイルは以下のページに格納されています。勉強の助けになれば幸いです。
また、線形回帰に関しては、本記事の内容は、最初の一歩のみを紹介しています。線形回帰を実際の研究や実務に利用したい方は、
以下の動画が大変参考になると思います。
2 解析方法
単回帰分析では、データによくあてはまる直線を考えます。以下に、そのイメージを示します。
直線は、数式で、y = ax+bという形で表すことができます。この直線を下の図では、緑で表しています。
単回帰分析では、この直線と、各サンプルとのちがい（残差）が最小になるような直線を求めます。
そのために、最小二乗法を用いていきます。
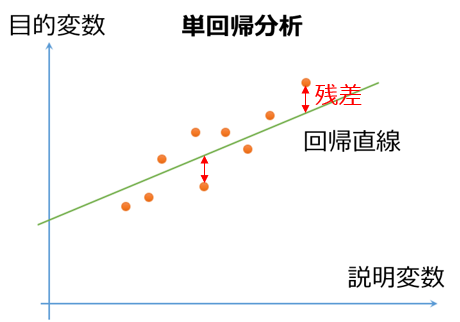
図出展：残差とは何か？正規分布していることの意味をわかりやすく解説！
最小二乗法については、以下の記事がわかりやすかったです。
3 導出
3.1. aとbについて偏微分
サンプルのyの値と、回帰式によって求められた値（予測値）との差が小さくなることを目的とします。
差分については、単純に引き算をすると、マイナスになった場合とプラスになった場合で誤差が相殺されてしまうため、
それらの2乗の値を考えます。そして、この誤差の2乗の値の和（残差平方和）が最小となる、aとbを求めたいと思います。
aとbとは、さきほど示したような、y = ax+bの式の傾きと切片のことです。
この残差平方和をEとします。また、のちの計算結果をよりシンプルにするため、1/2を係数として付けておきます。
...(1)
このEを最小とするために、aとbの値について微分（偏微分）をして、そのときの値がゼロになるときのことを考えます。
ここで、(1)の中に含まれる以下の部分をXと置きます。
...(2)
まずは、aについて偏微分することを考えます。
(2)のようにおいたため、(1)の式は、ある関数に別の関数が入っている関数になります。
そこで、以下のような、合成関数の微分を行います。
... (3)
式(2)をaで微分すると、であるため、(3)は以下のように展開できます。
...(4)
各項を個別に分けて、
...(5)
(5)のようになりました。
同様に、以下の(1)式をbで偏微分します。
...(1を再掲）
という式において、ここでも以下のようにXを定める。
...(2を再掲）
合成関数の微分の式は以下のようになる。
...(6)
(2)式において、bにて微分を行うと、1になるため、
...(7)
となり、さらに式を整理すると、
...(8)
...(9)
...(10)
このようになります。
3.2. 正規方程式を解く
3.1での偏微分の結果を整理すると以下のような2つの式（正規方程式）を得ることができます。
...(11)
...(12)
この(11)および(12)式を解くと、aとbの値、つまり、xとyの値が与えられたときの、
回帰式の傾きと切片を求めることができます。
(12)式の2項目はbNであるため、
...(13)
となります。この式をbについて解いて、
...(14)
を得ることができます。
この(14)を(11)に代入します。
...(15)
さらに、aについてまとめて、
...(16)
となります。
さらにaについて解くことで、
...(17)
となりました。この結果を(14)に代入して、
...(18)
となりました。これにより、傾きと切片の値を求めることができました。
4. コーディングをもとに検算
ここで、3章の結果が正しいかどうかを、実際にコーディングして確かめてみます。以下の3つの結果が同じになるかを検証します。
1 MATLABのregress関数にて、単回帰分析を行った場合の傾きと切片の値
2 Excelにて、単回帰分析を行った場合の傾きと切片の値
3 MATLABにて3章の結果を1から書いて計算させたときの、傾きと切片の値
4.1. MATLABのregress関数にて、単回帰分析を行った場合の傾きと切片の値
MATLABにて、デフォルトで読み込み可能な、examgradsデータを利用します。ここでは、データの内容については飛ばし、
傾きと切片の値が一致するかを検証します。
データをロードします。
load examgrades
yとXの値を設定します。
y = grades(:,5); X = [ones(size(grades(:,1))) grades(:,1)];
regress関数で単回帰分析を行います。
[mdl,~,r,rint] = regress(y,X);
傾きの値 0.3302
切片の値 50.2237
このように、傾きと切片の値をMATLABの関数で計算できました。次はExcelにて同様の計算を行います。
4.2 Excelにて、単回帰分析を行った場合の傾きと切片の値
4.1にて用いたデータをコピーアンドペーストして、「近似曲線」の機能を用いて、
傾きと切片の値を計算しました。
4.1と同じ、傾きと切片の値が計算されており、まずは、4.1および4.2で、ソフトウェアの関数や機能にてうまく値が計算できたと思われます。
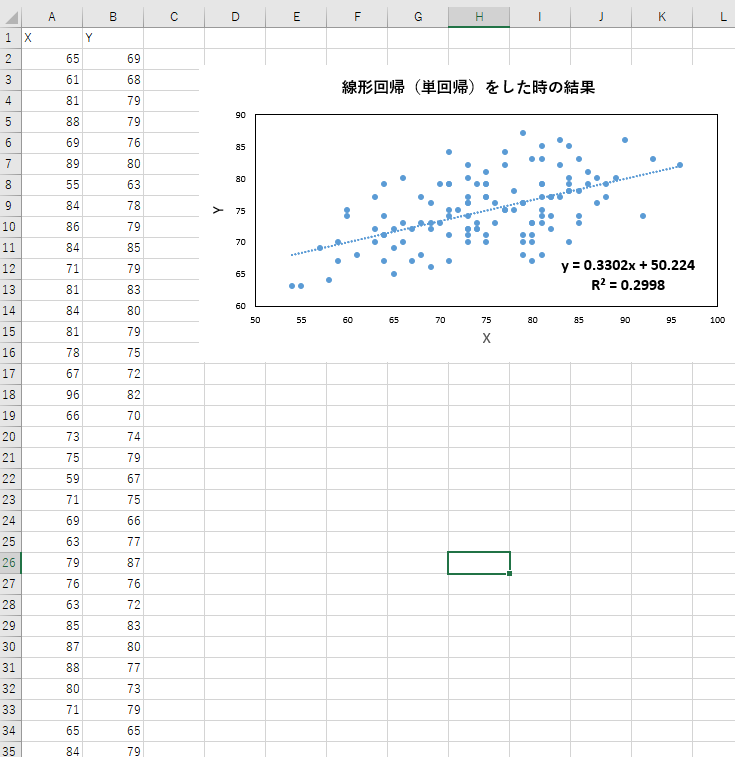
4.3 MATLABにて3章の結果を1から書いて計算させたときの、傾きと切片の値
ここが本番の計算です。さきほど導出した、(17) (18)式を用いて、傾きと切片の値を計算します。
...(17を再掲)
...(18を再掲)
以下のように短い行数で書いてみます。
x = grades(:,1); bunshi_a = sum(x.*y)-1/numel(x)*sum(x)*sum(y); bumbo_a = sum(x.^2)-1/numel(x)*(sum(x)^2); a = bunshi_a/bumbo_a
a = 0.3302
b = -1/numel(x)*sum(x)*a+1/numel(x)*sum(y)
b = 50.2237
さきほどの、4.1および4.2での結果と一致しました。3章での計算が正しかったと考えられます。
ひとまず、ここまでで、簡単にですが、単回帰分析について、第一段階の理解ができたことにします。
5. 行列を用いて解いた場合
4章では、3章の理解が正しいことを確かめることができました。
今回用いているMATLABでは、行列計算がやりやすいです。
そこで、3章で出てきた正規方程式を振り返ります。
...(11の再掲)
...(12の再掲)
上の連立方程式は、以下のように行列をもって表すことができます。
...(19)
逆行列を用いて、aとbは以下のように求めることができます。
...(20)
この計算は、以下のように簡単に実行可能です。
ab = inv([sum(x.^2) sum(x); sum(x) numel(x)])*[sum(x.*y);sum(y)]
ab = 2x1
0.3302
50.2237
このように、行列を用いた計算でも、正しく傾きと切片の値を計算できています。
今回は、単回帰分析で、変数が2つしかなかったため、3章のように解くことができましたが、
より多くの変数になると大変です。行列式を用いた導出や計算は非常に有効です。
6. 単回帰分析の性質の例
6.1 推定された回帰直線は、サンプルのxとyの平均を通る
切片の値は(14)で以下のように示されることがわかりました。
すると、回帰式は、
...(21)
となり、さらにaについて整理すると、
...(21)
となる。
および
は、xやyを全て足して、サンプル数で割った値、つまり平均です。
そのため、
y = a(x-xの平均)+(yの平均) となり、つまり、
推定された回帰直線は、サンプルのxとyの平均を通るということがわかります。
6.2 回帰残差の和はゼロとなる
単回帰分析にて、回帰を行っても、完全には説明できず、実際の値と、回帰した時の値の差（回帰残差 residual）が生まれます。
導出においては、この残差の二乗の和が最小になるようにしていました。
ここでは、この残差（2乗をしない）の和について考えます。
図出展：残差プロット
https://corvus-window.com/all_residual-plot/
以下のように、導出の段階で得た正規方程式を変形させてみます。
...(12の再掲)
...(22)
という式を得ることができました。
つまり、観測値yと回帰式によって得た値の差分をとり、それをサンプル数だけ足していくと0になります。つまり、
回帰残差の和はゼロとなることがわかりました。
6.3 回帰残差とxの値はベクトルとして直交している
6.2と同様に、以下の正規方程式を変形します。
...(11の再掲)
...(23)
つまり、回帰残差とxの値の内積がゼロであり、直交しているということを示しています。
7. 疑問点：線形回帰と主成分分析では何が異なるのか
主成分分析では、以下のように、その軸の分散が最大になるように、新たな軸を作っていました。
以下の図の、十字の軸は、線形回帰のときの回帰直線に似ています。
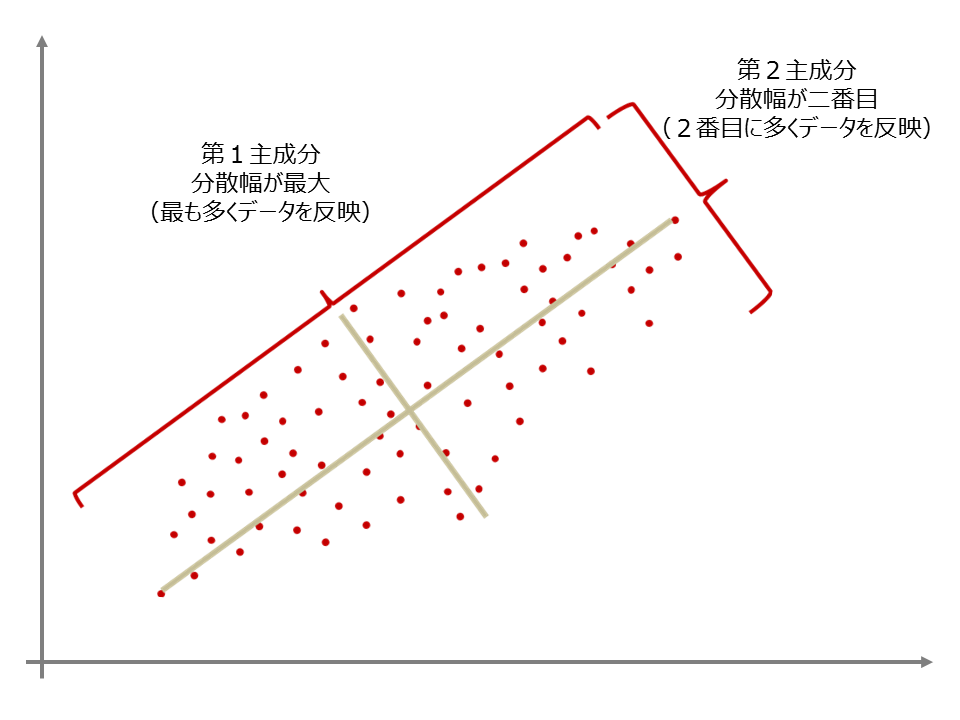
画像出典：株式会社インテージさま：主成分分析とは
https://www.intage.co.jp/glossary/401/
主成分分析については、私の過去の記事も見ていただけますと幸いです。
https://kentapt.hatenablog.com/entry/2022/02/16/182532
調べてみると、以下のようなわかりやすい資料がありました。
以下の文章および図は、浅野晃先生、応用統計学（2008 年度前期） 第６回(08. 5. 15)からの引用です。
=====引用開始=====
「分散が最大の軸」という表現で第１主成分を表現しましたが，もっと明確にいえば「多次元データを，それらがもつ価値をなるべく損なわないように，１次元の値（主成分得点）に縮約したもの」ということができます．また，図3 から明らかなように，第１主成分に投影することによって生じた価値の損失は，第２主成分によって表現されていることがわかります．ところで，この「各データと，その軸上への投影とのへだたりの２乗の合計が最小」という考え方は，回帰直線による直線のあてはめとよく似ています．回帰分析では，被説明変数の分散を，回帰直線からみた分散で何パーセント表現できるかを，回帰直線の当てはまり具合と考え，決定係数で表しました．しかし，両者の間には大きく違うところがあります（図5）．図3 からわかるように，主成分分析では，各データから第１主成分軸に垂線を下ろしたときの，各垂線の長さの２乗を最小にしています．これに対して，回帰分析では，各データから回帰直線に対してx1 軸に垂直に線分をひき，その長さの２乗を最小にしています．回帰分析では「x1 でx2 を説明する」あるいは「x1 からx2 を予想する」という考えにもとづいており，説明変数と被説明変数の区別があるので，x2 軸に沿ったへだたりを計算しています．主成分分析ではこのような区別はなく，どちらでどちらを説明しているわけでもないので，軸と各データとの「距離」を最小化の対象としています．
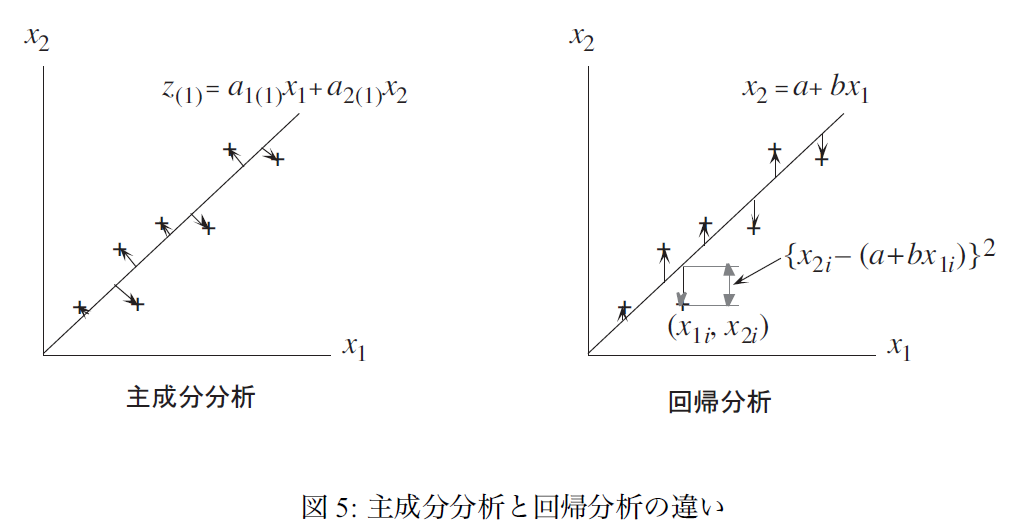
=====引用終了=====
「回帰分析では「x1 でx2 を説明する」あるいは「x1 からx2 を予想する」という考えにもとづいており」という点と、主成分分析ではそのような関係は想定しておらず、新たな主成分軸と各データとの距離そのものに主眼がおかれている、という点が納得がいき、非常に勉強になりました。
以下の、記事でも、回帰直線への垂線の長さを最小化する問題を解くと、ラグランジュの未定乗数法に
https://takmin.hatenablog.com/entry/2020/09/17/135353
8. その他：ガウスとルジャンドルとの論争
最小二乗法の発見に関しては以下のようなストーリーがあるそうです。以下の文章は入門統計学から引用しています。
=====引用開始=====
最小二乗法は、ドイツの天才学者であるガウスが小惑星セレスの軌道の計算に使ったことが始まりであると現在では知られています(1801年)。しかしガウスは自分の業績を公表することに無頓着でした。そのため、ルジャンドルというフランスの数学者がガウスよりも先（1805年）に論文として同様の理論を発表してしまい、他の数学者も巻き込んでの大論争になってしまいました。
=====引用終了=====
9. 簡単なまとめ
この記事では、1変数のみの回帰直線の係数の計算方法（単回帰による回帰直線の傾きと切片の計算方法）についてまとめました。
私の理解による結果と、MATLABやExcelによる計算結果が一致しており、よかったです。
決定係数といった他の重要な事項に触れることができませんでしたが、今回は記事が長くなってしまったため、ひとまずここで一区切りとしたいと思います。今回の勉強にあたり、本文にて紹介した皆様の情報が非常に頼りになりました。ありがとうございました。
10. 参考文献（本文中に記載のないもの）
最小二乗法の基礎を丁寧に
回帰直線の式を最小二乗法により計算する
永田靖、棟近雅彦共著：多変量解析入門
多変量解析法入門 (ライブラリ新数学大系) | 靖, 永田, 雅彦, 棟近 |本 | 通販 | Amazon
東京大学教養学部統計学教室 (編集) 統計学入門 (基礎統計学Ⅰ)
統計学入門 (基礎統計学Ⅰ) | 東京大学教養学部統計学教室 |本 | 通販 | Amazon
最小二乗法① 数学的性質 経済統計分析 (2013年度秋学期)
http://www2.toyo.ac.jp/\textasciitilde{}mihira/keizaitoukei2014/ols1.pdf
MATLABドキュメンテーション：regress
iPhone LiDARで取得した3次元点群を地図上にプロットしてみよう
この記事は、MATLABアドベントカレンダー3日目の記事として書かれています。
この記事では、iPhone LiDARで取得した3次元点群をMATLABにて読み込み、さらに、地図（地球）上で可視化する方法について紹介します。言語はMATLABを使用します。
3次元点群を取得するためのアプリはScaniverseを用いました。
詳しい使い方は、以下の記事がわかりやすかったです。ここでは、すでにiPad LiDARにて計測し、PCに転送した状態から始めます。
PCに転送（エキスポート）する方法は以下の図の通りです。右下のShareボタンから行うことができます。
なお、3次元モデルをエキスポートする際は、一番下のLAS形式を選択してください。
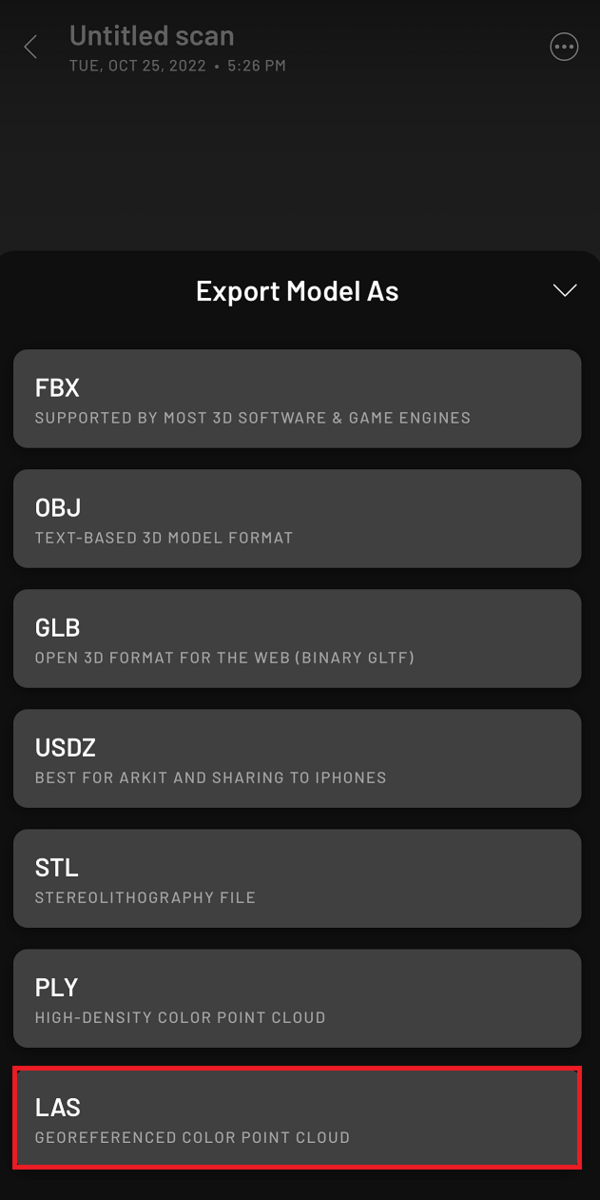
なお、ここで用いたコードや、点群ファイルは以下のページにアップロードされています。ぜひ、ダウンロードしてお使いください。
点群ファイルの読み込み
LiDAR toolboxの機能を用いて、点群データの読み込みを行います。以下のように、lasFileReaderやreadPointCloud関数を用いて、簡単に点群ファイルを読み込むことができます。
clear;clc;close all % las/lazファイルを読み込むためのlasFileReader objectを作成する lasReader = lasFileReader('treeTrunk.laz'); % las/lazファイルの、xyzおよび色情報を読み込み ptCloud = readPointCloud(lasReader); % 可視化 figure('Visible','on');pcshow(ptCloud)
以下のように、複雑な3次元形状を有する、樹木の幹部分をきれいに点群化できていることがわかります。iPhone LiDARとアプリ（Scaniverse）を用いることで、お手軽にこのようにきれいな点群を取得できるのは素晴らしいです。
座標系の変換
projcrsオブジェクトの作成
2022年12月においては、Scaniverseで、点群を取得し、エキスポートする場合（LAS形式）、経度・緯度ではなく、2次元平面に投影した方式でxy座標が保存されます。
具体的には、点群の座標は、東京で取得された場合、UTM N54（EPSGコード：32654）でエキスポートされます。後で用いる、geoplot関数との兼ね合いのため、これを経度・緯度に変換します。
projcrs関数に、EPSGコードを入力します。その結果、projcrsオブジェクトを作成することができます。
% projcrsオブジェクトを作成する utm54N = projcrs(32654); % 確認のため、CRSを表示 utm54N.GeographicCRS.Name
ans = "WGS 84"
UTMは、ユニバーサル横メルカトル（Universal Transverse Mercator）の略です。地球はおおよそ球形で、地球上の対象の座標は、3次元的に表すことができますが、それを2次元平面の投影しています。UTMはその投影方法の1つです。詳しい内容については、以下のページをご参照ください。
projcrsオブジェクトの中身は以下のようになっています。Nameには、投影方法が書いています。lengthUnitでは、単位（メートル）が、ProjectionMethodには、投影方法が書いています。
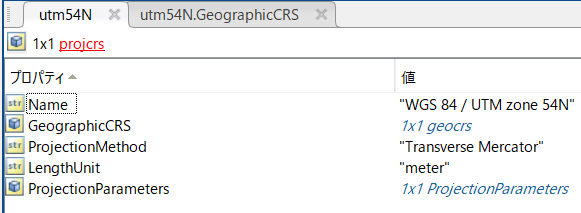
さらに、ここの、GeographicCRSは、geocrsオブジェクトが格納されており、その中身は以下のようになっています。
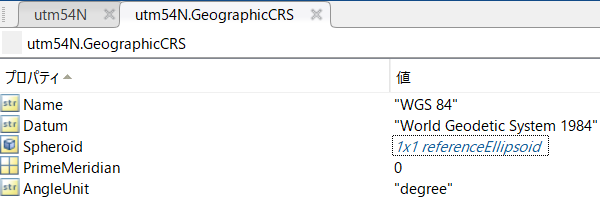
WGS 84についてですが、地球はおおよそ球体をしており、それを数式などを使ってモデル化することで、測量を行うことができます。そのモデル化の方式には、日本測地系や世界測地系といった様々なものがあります。WGS 84は世界測地系の中の1つの方式です。
この説明については、以下のページがわかりやすかったです。
経度・緯度への変換
ここまで、iPhone LiDARの結果の表現に用いられた投影方法を表すオブジェクトを作成していました。次は、projinv関数を用いて、utm54Nのxy座標を経度・緯度に変換します。経度・緯度に変換することで、簡単に地図上にiPhone LiDARの点群の情報をプロットすることができます。
そして、この結果の可視化は、geoplot関数で行うことができます。
[lat,lon] = projinv(utm54N,ptCloud.Location(:,1),ptCloud.Location(:,2)); figure; geoplot(lat,lon) % hold on;geobasemap('streets') hold on;geobasemap('topographic')
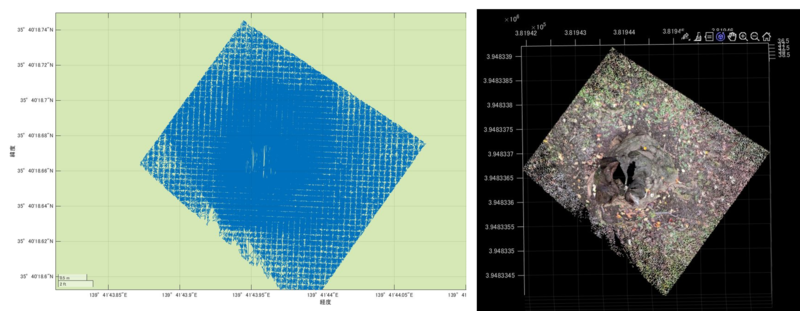
上のようなプロットができましたが、これではどういう情報がプロットされているのかよくわかりません。もう少しズームアウトしてみます。
地図の上に、さきほどの樹木の幹の点群がプロットされていることがわかります。位置に関しても、この点群が取得された、東京都の代々木公園に正しくプロットされています。
ベースマップ（地図の種類）を変更するために、以下のように、geobasemapの中身を他のベースマップの種類を指定することもできます。
geobasemap('topographic')
さきほどの初めの図は少しわかりにくかったですが、このプロットの結果は樹木の点群を上から見た時の様子を示しているものだとわかります。
3次元マップでの点群の可視化
さきほどは、地図上にて、点群を可視化しましたが、2次元のマップであったため、各点の位置やその上からの様子を知るということに限定されていました。これでは、iPhone LiDARで取得した3次元情報をうまく可視化できているとは言えません。このセクションでは、iPhone LiDARで取得した点群を、3次元のマップ上で可視化してみます。
% 25点のうち1点のみを表示する。重くなってしまうため。 mskip = 1:25:length(lat); % 3Dで可視化するための図を用意する uif = uifigure; g = geoglobe(uif); % プロット geoplot3(g,lat,lon,ptCloud.Location(:,3)-mean(ptCloud.Location(:,3)),'r','MarkerSize',2,'Marker','o','HeightReference','terrain','LineStyle','none','MarkerIndices',mskip)
可視化している様子は以下の動画をご覧ください。
このように、3Dの地図（ベースマップ）上で、iPhone LiDARの点群を可視化することができました。
色はうまく表示できていませんが、ベースマップ上でどのような点群が取得されたかを確認することができます。
いくつか注意点があるので記述します。
-
r:プロットの色。各点を実際の3Dの色付けを行うことができない。指定した1つの色のみの可視化になる -
'LineStyle','none': これにより、独立した点（線でない）をプロットできる -
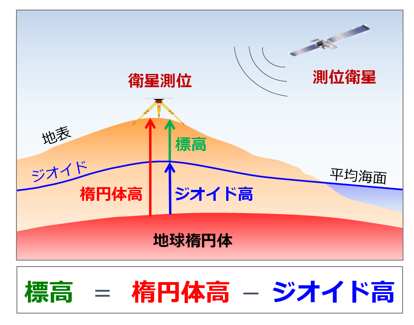
'HeightReference','terrain': 高さの基準を設定する。このほかに、'geoid'や'ellipsoid'が選択可能である。それぞれの違いについては、以下の図を参照して下さい。 -
'MarkerIndices'にて間引きを行わないと、表示が非常の重くなるため注意する必要がある。
まとめ
- この記事では、iPhone LiDARで取得した点群をMATLABを用いて、地図上で可視化しました
- 投影座標系から経度・緯度への変換も簡単に行うことができました
- 3Dのベースマップ上で、点群を可視化することができました
- 表示する点数が多くなると、非常にビューワーが重くなるため、間引くことが必要です
- 容量の大きな点群や色付きの点群を閲覧することが難しいという課題はありますが、3次元データをスマホで取得し、お手軽にMATLABで遊べるという点が非常によかったです
参考にしたページ（本文中に記載がないもの）
FLIRカメラで取得した熱画像をRGB画像に変換してみよう
1. はじめに
この記事では、FLIR社の赤外線カメラを用いて、取得した画像をRGB画像に変換する方法について述べます。ここでは、Pythonを用います。
赤外線カメラの詳細や、そのカメラの応用事例については以下のページが参考になりました。
本記事では、FLIR社製の赤外線カメラを用います。以下に、そのカメラの例を掲載します。
画像出展
FLIR社の赤外線カメラで取得した画像の例を以下に示します。温度によって、色分けされて示されています。この画像では、約22度から27度の範囲の温度が観測されています。
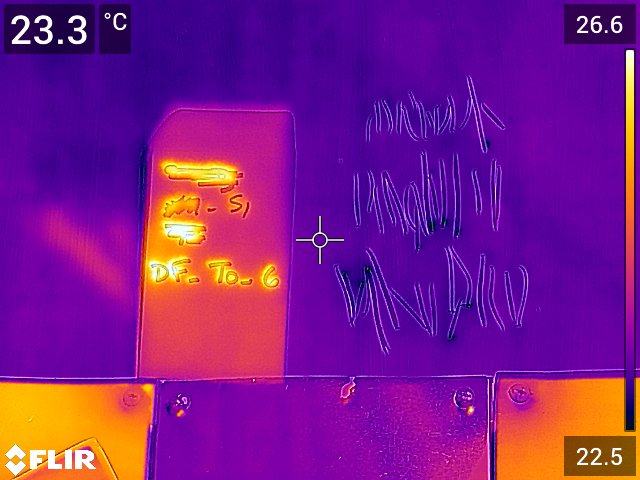
また、このカメラは、同時にRGB画像（色画像）を取得している場合が多く、この温度情報を持った画像をRGB画像に変換することができます。
その変換は、以下のFLIR Toolsと呼ばれるソフトウェアを用いて行うことができます。FLIR Toolsのインストール方法は以下のページをご覧ください。
また以下の動画もわかりやすかったです。
このソフトウェアを用いて、以下のように、赤外線カメラの画像をRGB画像に変換することができます（以下の図はイメージです）。
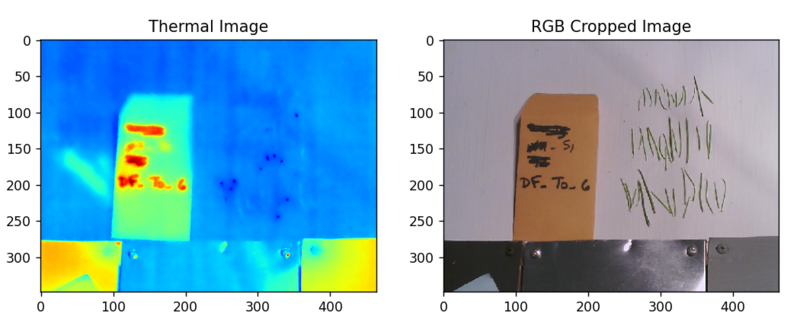
また、各ピクセルの持つ温度の値もCSVファイルとして取り出すことができます。
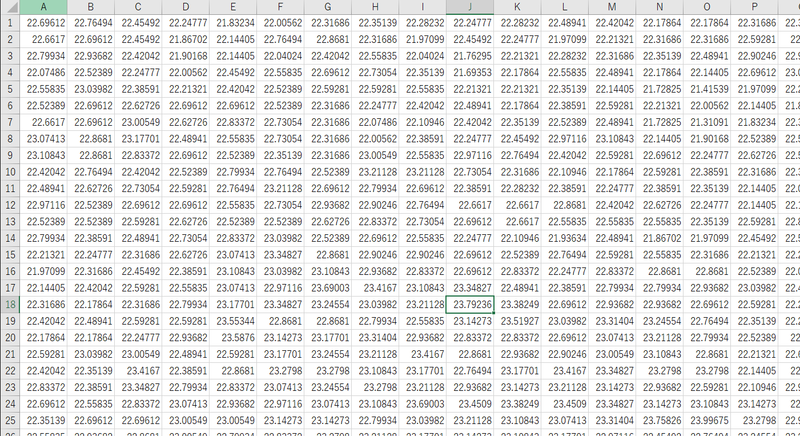
しかし、FLIR Toolsでは、1枚ずつ、読み込み、作業をすることが必要で、大量の画像をまとめて、同じ処理を繰り返すことは難しいです。
そこで、本記事では、以下のレポジトリを用いて、赤外線カメラの画像を、RGB画像に変換し、さらに、温度情報のCSVファイルを自動保存する方法について述べます。
なお、本記事で用いている画像やコードも以下のレポジトリのサンプルを用いています。
また、上のレポジトリをフォークし、少しアレンジを加えたものが以下のページで、本記事で用いるコードや原稿はここにアップロードされています。
2. 環境構築について
2.1. Exif toolのダウンロード
exiftoolの概要やそのダウンロードの方法や使い方は以下のページに記載しています。
exiftoolを用いて、赤外線カメラの画像のメタ情報を取得した時の結果の例です。取得したカメラのモデル情報なども記載されていることがわかります。
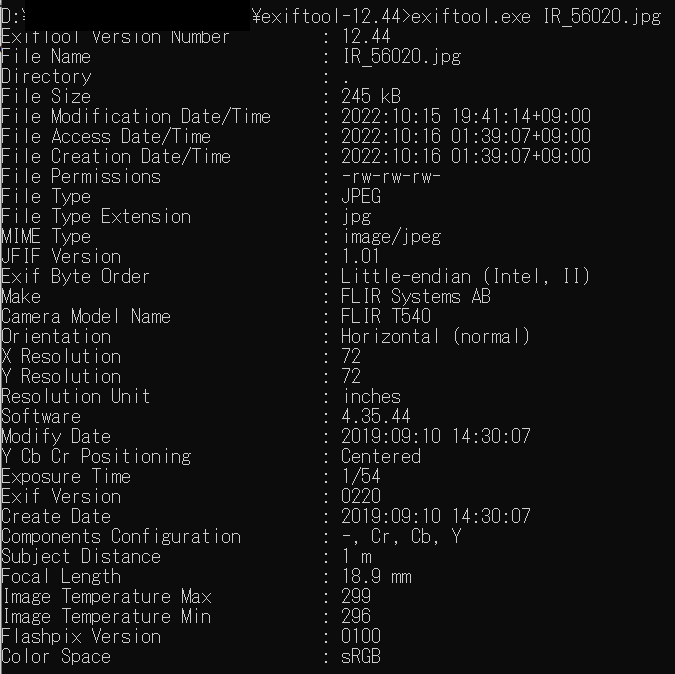
2.2. Pythonの実行環境について
まずは、このレポジトリのファイルをダウンロードします。
環境構築については、以下の2つの方法を紹介します。
- 必要なパッケージをインストールする
- 私の作ったanaconda環境をそのまま自分のPCに複製する
2の方法が簡単ですが、OSの違いなどで複製できない場合もあるため、1から説明します。
2.2.1. 必要なパッケージをインストールする
1. pythonのインストール
ここでは、python3.7を用いた。OSはWindowsを使用。
2. flirimageextractorのインストール
pip install flirimageextractor
にて、flirimageextractorをインストールする
3. その他、コードを実行しながら、必要なパッケージをインストールする
3章で示すコマンドにて、必要なパッケージを適宜インストールしてください。
2.2.2. この記事で用いたanaconda環境をそのまま自分のPCに複製する
さきほど述べたように、以下のレポジトリをダウンロード、または、クローンし、envフォルダの中にenv.ymlが存在していることを確認します。
以下のページにあるように、
conda env create -n 新たな環境名 -f ファイル名.yml
で、環境の複製が可能です。
今回の場合は、env.ymlが存在しているフォルダに移動し、
conda env create -n myEnv -f env.yml
を実行することで環境の複製を行うことができます。
3. メインコードの実行
3.1. exiftoolのパスの設定
demo.pyの35行目周辺に以下のコードがあります。ご自身のexiftoolのパスに置き換えてください。Dドライブではなく、Cドライブにexiftoolを置くほうがよいかもしれません。
exiftoolpath = "C:\Program Files (x86)\exif\exiftool.exe”
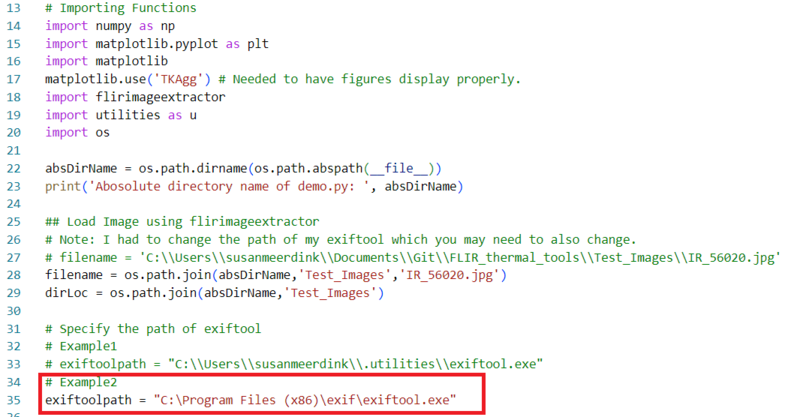
3.2. demo.pyの実行
demo.py や utilities.py のあるディレクトリで、demo.pyを実行すると、Test_Imagesフォルダ内の画像に対して、テストコードが実行されます。特に引数の設定は必要ありません。
私はAnaconda環境を用いているため、Anaconda Promptから実行しています。
このコードにより、熱画像からRGB画像およびCSVファイルの保存を行います。
また、以下のような画面が出てくれば、左の赤外線画像と右のRGB画像の順に、右クリックで、対応している点を選びます。できるだけ多くの対応点を選択し、エンターボタンを押してください。
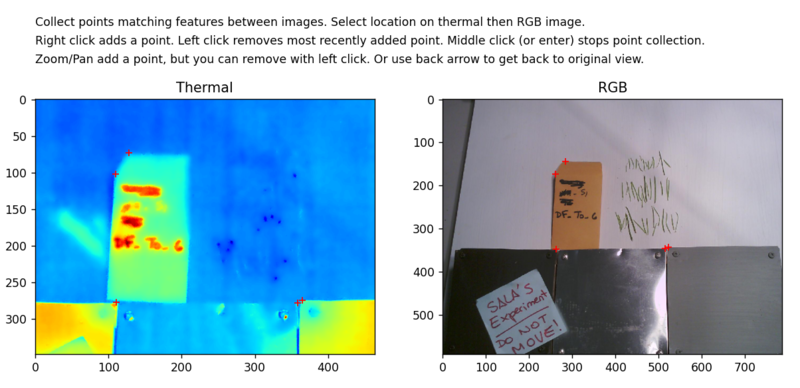
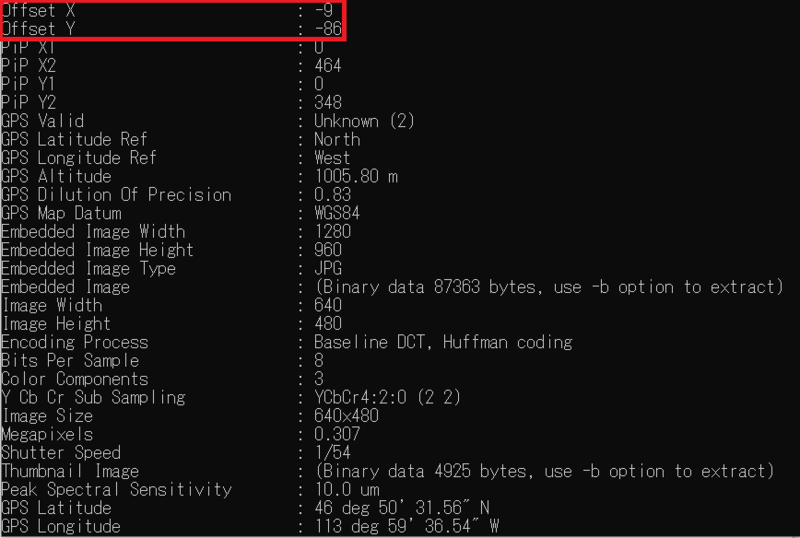
赤外線カメラの画像と、そのRGB画像には、ずれ（offset）があり、補正をする必要があります。上で述べた、exiftoolsをつかって、そのoffset値を読み取ることもできるのですが、必ずしもぴったりといくわけではなく、手動による補正が必要な場合もあるようです。
これにより、FLIR社製の赤外線カメラの画像をRGB画像に変換し、さらに、その温度情報をCSVファイルに書き込むことができます。
4. まとめ
この記事では、Pythonを用いて、FLIRの赤外線カメラの画像からRGBおよび、温度情報を表す、CSVファイルを取得することができました。この方法を用いて、経時的に取得した大量の画像や、多視点からの画像を自動的に処理できそうです。
